GradientFittedMesh
GradientFittedMesh[{p1,p2,…}]
gives a MeshRegion whose gradient best fits the normals at points p1,p2,….
Details and Options

- GradientFittedMesh is also known as Poisson surface reconstruction.
- GradientFittedMesh is typically used to construct closed smooth regions from a set of points with normals.
- GradientFittedMesh gives a MeshRegion that approximates a geometric region with a scalar indicator function
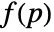 whose gradient
whose gradient 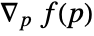 best fits the normals ni at the points pi.
best fits the normals ni at the points pi. - GradientFittedMesh finds the best least-squares approximate solution
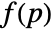 whose Laplacian equals the divergence of the normals
whose Laplacian equals the divergence of the normals 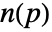 .
. - Vertex normals ni for points pi can be specified by Point[{p1,p2,…},VertexNormals{n1,n2,…}].
- In GradientFittedMesh[{p1,p2,…}], normals to the points pti are estimated by computing the least-squares fit plane on the nearest neighboring points.
- GradientFittedMesh takes the same options as MeshRegion, with the following additions and changes:
-
PerformanceGoal $PerformanceGoal aspects of performance to try to optimize VertexNormals Automatic vertex normals to use

Examples
open allclose allBasic Examples (2)
Scope (2)
GradientFittedMesh works on coordinates:
It is equivalent to points without normals:
GradientFittedMesh works on oriented points:
Options (2)
VertexNormals (1)
Specify coordinate orientations using VertexNormals:
Applications (1)
Possible Issues (1)
GradientFittedMesh only works on 3D points:
Text
Wolfram Research (2021), GradientFittedMesh, Wolfram Language function, https://reference.wolfram.com/language/ref/GradientFittedMesh.html.
CMS
Wolfram Language. 2021. "GradientFittedMesh." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GradientFittedMesh.html.
APA
Wolfram Language. (2021). GradientFittedMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GradientFittedMesh.html