WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

Point
✖
Point

✖
Point[p]

is a graphics and geometry primitive that represents a point at p.

✖
Point[{p1,p2,…}]

represents a collection of points.

Details and Options

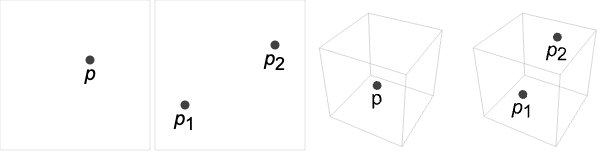
Background & Context

  • Point is a graphics and geometry primitive that represents a geometric point. The position of a Point in 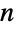-dimensional space is specified as a list argument consisting of 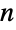Cartesian coordinate values, where RegionEmbeddingDimension can be used to determine the dimension 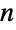for a given Point expression. A collection of points may be represented as a list of 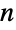-tuples inside a single Point primitive (a "multi-point"). The coordinates of Point objects may have exact or approximate values.
  • Point objects can be visually formatted in two and three dimensions using Graphics and Graphics3D, respectively. Point objects can also be used in geographical maps using GeoGraphics and GeoPosition (e.g. GeoGraphics[Point[GeoPosition[{38.9,-77.0}]]]). Finally, Point may serve as a region specification over which a computation should be performed.
  • While points themselves have dimension 0 (as reported by the RegionDimension function), Point objects in formatted graphics expressions are by default styled to appear "larger" than a 0-dimensional mathematical point. Furthermore, in graphical visualizations, points are displayed at the same size regardless of possibly differing distances from the view point. The appearance of Point objects in graphics can be modified by specifying sizing directives such as PointSize and AbsolutePointSize, color directives such as Red, the transparency directive Opacity, and the style option Antialiasing. In addition, the colors of multi-points may be specified using VertexColors, while the shading and simulated lighting of multi-points within Graphics3D may be specified using VertexNormals.
  • GeometricTransformation and more specific transformation functions such as Translate and Rotate can be used to change the coordinates at which a Point object is displayed while leaving the underlying Point expression untouched.
  • Other graphics primitives such as Circle, Disk, Sphere, and Ball may resemble those of stylized Point objects. Locator is another point-like interactive object that represents a draggable locator object in a graphic.
  • While the Point primitive explicitly appears in graphics and geometric region specification expressions, it should be noted that coordinates are commonly represented as bare lists in other contexts in the Wolfram Language. Examples of this type include coordinate specifications appearing inside other graphics primitives (e.g. Line[{{0, 0},{1,1}}]), arguments to Locator (e.g. Graphics[Locator[{0,2}]]), and when using Nearest to compute a nearest point. A number of functions (e.g. RegionNearest, RegionCentroid, ArgMin, and ArgMax) also naturally return bare lists of coordinates as opposed to explicit Point objects, while others (e.g. Solve and NSolve) return solution "points" as lists of variable replacement rules (e.g. ).

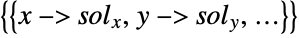Examples

open allclose all

Basic Examples  (5)Summary of the most common use cases

A single point:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-gm9ld1
Out[1]=1

Multiple points:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-byks65
Out[1]=1

Points in 3D:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-c97m4w
Out[1]=1

Differently styled points:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-jxuv9k
In[2]:=2
✖
https://wolfram.com/xid/0gismq-kptuq4
Out[2]=2

Count and centroid:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-f11tmy
In[2]:=2
✖
https://wolfram.com/xid/0gismq-ex61ol
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0gismq-zp4gqg
Out[3]=3

Scope  (20)Survey of the scope of standard use cases

Graphics  (10)

Specification  (2)

A single point:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-nwfg7d
Out[1]=1

Multiple points:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-bsitbs
Out[1]=1

Styling  (5)

Points with different sizes:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-bg0zkd
In[2]:=2
✖
https://wolfram.com/xid/0gismq-gpdc62
Out[2]=2

Scaled point size:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-htdish
In[2]:=2
✖
https://wolfram.com/xid/0gismq-kh0wjg
Out[2]=2

Point size in printer's points:

In[3]:=3
✖
https://wolfram.com/xid/0gismq-d56vnj
Out[3]=3

Colored points:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-we3x
In[2]:=2
✖
https://wolfram.com/xid/0gismq-mkj8z0
Out[2]=2

Colors can be specified at vertices using VertexColors:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-cn0av
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0gismq-gff7zx
Out[2]=2

Normals can be specified at vertices using VertexNormals for 3D points:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-hqxpxd
Out[1]=1

Coordinates  (3)

Use Scaled coordinates:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-s6971
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0gismq-barlp9
Out[2]=2

Use ImageScaled coordinates in 2D:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-ezd7wr
Out[1]=1

Use Offset coordinates in 2D:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-hv1ouf
Out[1]=1

Regions  (10)

Embedding dimension is the dimension in which the points live:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-mha969
In[2]:=2
✖
https://wolfram.com/xid/0gismq-y220
Out[2]=2

The geometric dimension of a point is always 0:

In[3]:=3
✖
https://wolfram.com/xid/0gismq-bx9tom
Out[3]=3

Point membership test:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-0nrvj5
In[2]:=2
✖
https://wolfram.com/xid/0gismq-y2qpwa
Out[2]=2

Get conditions for point membership:

In[3]:=3
✖
https://wolfram.com/xid/0gismq-2p4iz
Out[3]=3

The measure of a set of points is the counting measure:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-5ht44k
In[2]:=2
✖
https://wolfram.com/xid/0gismq-z6qch
Out[2]=2

Centroid:

In[3]:=3
✖
https://wolfram.com/xid/0gismq-dxlbau
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0gismq-lgbg4z
Out[4]=4

Distance to a set of points:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-oc6hy
In[2]:=2
✖
https://wolfram.com/xid/0gismq-bjikjq
Out[2]=2

Signed distance from a point:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-cybvpc
In[2]:=2
✖
https://wolfram.com/xid/0gismq-bm4ed
Out[2]=2

Nearest point in the region:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-btejnv
In[2]:=2
✖
https://wolfram.com/xid/0gismq-et4yza
Out[2]=2

Nearest points:

In[3]:=3
✖
https://wolfram.com/xid/0gismq-eoyt0e
In[4]:=4
✖
https://wolfram.com/xid/0gismq-fq1ssz
Out[4]=4

A point set is bounded:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-5w7bb1
In[2]:=2
✖
https://wolfram.com/xid/0gismq-b5d6xy
Out[2]=2

The bounding range:

In[3]:=3
✖
https://wolfram.com/xid/0gismq-czy13e
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0gismq-dibg56
Out[4]=4

Integrate over a three-point set using the counting measure:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-fivgav
In[2]:=2
✖
https://wolfram.com/xid/0gismq-banwkr
Out[2]=2

An equivalent way:

In[3]:=3
✖
https://wolfram.com/xid/0gismq-m3ci6o
Out[3]=3

Optimize over a three-point set:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-nf9ton
In[2]:=2
✖
https://wolfram.com/xid/0gismq-hyz4dq
Out[2]=2

Solve equations in a 1000-point set:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-bnrw6
In[2]:=2
✖
https://wolfram.com/xid/0gismq-c7lkth
Out[2]=2

Options  (3)Common values & functionality for each option

VertexColors  (2)

Point with vertex colors:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-dho4ih
Out[1]=1

Specify vertex colors for 3D points:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-c2ui4p
Out[1]=1

VertexNormals  (1)

Specify vertex normals for 3D points:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-eg67w
Out[1]=1

Applications  (5)Sample problems that can be solved with this function

Use Point to indicate features, e.g. zeros of a function:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-kx8xvv
Out[1]=1

A simple point classification, visualized using Point:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-ivixus
In[2]:=2
✖
https://wolfram.com/xid/0gismq-gha0z
Out[2]=2

The same idea in 3D:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-mly0n1
In[2]:=2
✖
https://wolfram.com/xid/0gismq-e1w5xq
Out[2]=2

Visualize the result of cluster analysis:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-c7x5qf
In[2]:=2
✖
https://wolfram.com/xid/0gismq-fh1xc
In[3]:=3
✖
https://wolfram.com/xid/0gismq-meqrw9
Out[3]=3

Replace Polygon with Point to have special rendering effects:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-be8jvg
In[2]:=2
✖
https://wolfram.com/xid/0gismq-cdo5kc
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0gismq-b3vhao
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0gismq-gbnh8s
In[5]:=5
✖
https://wolfram.com/xid/0gismq-hrqt9t
Out[5]=5

Properties & Relations  (2)Properties of the function, and connections to other functions

Use ListPlot to visualize 1D sequences:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-klmpk3
Out[1]=1

Use ListPointPlot3D to visualize 2D sequences:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-bisehf
Out[1]=1

Possible Issues  (1)Common pitfalls and unexpected behavior

PointSize is a scaled size that refers to the width of the graphic:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-b7qx7s
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0gismq-eijg0o
Out[2]=2

Use AbsolutePointSize to control the size:

In[3]:=3
✖
https://wolfram.com/xid/0gismq-dnu1j2
Out[3]=3

Neat Examples  (3)Surprising or curious use cases

A random point collection:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-hlrki4
Out[1]=1

Points on the unit sphere with correct normals:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-fbo9pb
Out[1]=1

Disperse a grid of points from a moving center:

In[1]:=1
✖
https://wolfram.com/xid/0gismq-jz7lj9
Out[1]=1
Wolfram Research (1988), Point, Wolfram Language function, https://reference.wolfram.com/language/ref/Point.html (updated 2014).
✖
Wolfram Research (1988), Point, Wolfram Language function, https://reference.wolfram.com/language/ref/Point.html (updated 2014).

Text

Wolfram Research (1988), Point, Wolfram Language function, https://reference.wolfram.com/language/ref/Point.html (updated 2014).

✖
Wolfram Research (1988), Point, Wolfram Language function, https://reference.wolfram.com/language/ref/Point.html (updated 2014).

CMS

Wolfram Language. 1988. "Point." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Point.html.

✖
Wolfram Language. 1988. "Point." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Point.html.

APA

Wolfram Language. (1988). Point. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Point.html

✖
Wolfram Language. (1988). Point. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Point.html

BibTeX

@misc{reference.wolfram_2025_point, author="Wolfram Research", title="{Point}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Point.html}", note=[Accessed: 26-March-2025 ]}

✖
@misc{reference.wolfram_2025_point, author="Wolfram Research", title="{Point}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Point.html}", note=[Accessed: 26-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_point, organization={Wolfram Research}, title={Point}, year={2014}, url={https://reference.wolfram.com/language/ref/Point.html}, note=[Accessed: 26-March-2025 ]}

✖
@online{reference.wolfram_2025_point, organization={Wolfram Research}, title={Point}, year={2014}, url={https://reference.wolfram.com/language/ref/Point.html}, note=[Accessed: 26-March-2025 ]}