GradientFittedMesh
GradientFittedMesh[{p1,p2,…}]
给出一个 MeshRegion,其梯度最适合点 p1,p2,… 的法线.
更多信息和选项

- GradientFittedMesh 也称为泊松表面重建.
- GradientFittedMesh 通常用于从一组具有法线的点构建封闭的平滑区域.
- GradientFittedMesh 给出一个 MeshRegion,它用标量指示函数
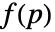 逼近几何区域,其梯度
逼近几何区域,其梯度 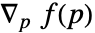 最适合点 pi 处的法线 ni.
最适合点 pi 处的法线 ni. - GradientFittedMesh 找到最佳最小二乘近似解
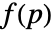 ,其拉普拉斯算子等于法线的散度
,其拉普拉斯算子等于法线的散度 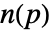 .
. - 点 pi 的顶点法线 ni 可以通过 Point[{p1,p2,…},VertexNormals{n1,n2,…}] 指定.
- 在 GradientFittedMesh[{p1,p2,…}] 中,点 pti 的法线通过计算最近相邻点上的最小二乘拟合平面来估计.
- GradientFittedMesh 采用与 MeshRegion 相同的选项,但有以下添加和更改:
-
PerformanceGoal $PerformanceGoal 要尝试优化的性能方面 VertexNormals Automatic 要使用的顶点法线

范例
打开所有单元关闭所有单元
Wolfram Research (2021),GradientFittedMesh,Wolfram 语言函数,https://reference.wolfram.com/language/ref/GradientFittedMesh.html.
文本
Wolfram Research (2021),GradientFittedMesh,Wolfram 语言函数,https://reference.wolfram.com/language/ref/GradientFittedMesh.html.
CMS
Wolfram 语言. 2021. "GradientFittedMesh." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/GradientFittedMesh.html.
APA
Wolfram 语言. (2021). GradientFittedMesh. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GradientFittedMesh.html 年