GraphAssortativity

GraphAssortativity[g]

使用顶点度给出图 g 的协同性系数.

GraphAssortativity[g,"prop"]

使用顶点特性 "prop" 给出图 g 的协同性系数.

GraphAssortativity[g,{{vi 1,vi 2,…},…}]

给出关于顶点划分 {{vi 1,vi 2,…},…} 的图 g 的协同性系数.

GraphAssortativity[g,{v1,v2,…}{x1,x2,…}]

对顶点 {v1,v2,…} 使用数据 {x1,x2,…} 给出图 g 的协同性系数.

GraphAssortativity[{vw,…},…]

使用规则 vw 来指定图 g.

更多信息和选项

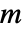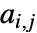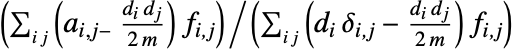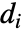  • 对于具有 条边和邻接矩阵元素为 的图，协同性系数由 给出，其中 是顶点 vi 的出度，如果存在从 vi 到 vj 的边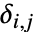， 等于 1，否则等于 0.
  • 对于使用 x1,x2,… 的数量数据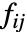， 等于 xixj.
  • 对于使用 x1,x2,… 的类别数据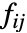， 等于 1（如果 xi 和 xj 相等），否则为 0.
  • 在 GraphAssortativity[g] 中，xi 是顶点 vi 的顶点出度.
  • 在 GraphAssortativity[g,"prop"] 中，对于顶点 vi，xi 等于 AnnotationValue[{g,vi},"prop"].
  • 在 GraphAssortativity[g,{{vi 1,vi 2,…},…}] 中，子集 {vi 1,vi 2,…} 中的顶点具有相同的类别数据 xi 1=xi 2=….
  • GraphAssortativity[g,Automatic->{x1,x2,…}] 的顶点列表是 VertexList[g].
  • 选项 "DataType"->type 可以用于指定数据 x1,x2,… 的类型. 可能的设置是 "Quantitative" 和 "Categorical".
  • 选项 "Normalized"->False 可用于计算协同性的模块性.
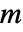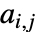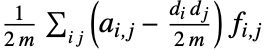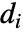  • 对于具有 条边和邻接矩阵元素为 的图，协同性模块性由 给出，其中 是顶点 vi 的出度.
  • GraphAssortativity 可用于无向图、有向图、加权图、多图和混合图.

范例

打开所有单元关闭所有单元

基本范例  (2)

计算 Zachary 跆拳道俱乐部网络的协同性系数：

均匀随机图的协同性系数分布：

范围  (12)

GraphAssortativity 可用于无向图：

有向图：

加权图：

多图：

混合图：

使用规则指定图：

使用顶点特性数据计算协同性系数：

顶点划分：

特定数据集：

VertexList 的子集的划分或者赋值：

GraphAssortativity 可用于符号式表达式：

GraphAssortativity 可用于大型图：

应用  (3)

根据顶点颜色笔记顶点划分的协同性系数：

根据友情网络中朋友数目求异配性：

网络划分显示协同性混合：

高中的友情网络，顶点使用种族配色. 分析学生与其他相似的人联系的爱好：

高度活跃的学生是其他高度活跃的学生的朋友：

学生与同种族的学生之间体现出正趋向性：

属性和关系  (2)

协同性系数位于 -1 和 1 之间：

完美的协同图：

完全异配图：

GraphAssortativity 是连通顶点之间的度数的 Pearson 相关系数：

Correlation 给出 Pearson 相关系数：

Wolfram Research (2012)，GraphAssortativity，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GraphAssortativity.html （更新于 2015 年）.

文本

Wolfram Research (2012)，GraphAssortativity，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GraphAssortativity.html （更新于 2015 年）.

CMS

Wolfram 语言. 2012. "GraphAssortativity." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/GraphAssortativity.html.

APA

Wolfram 语言. (2012). GraphAssortativity. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GraphAssortativity.html 年

BibTeX

@misc{reference.wolfram_2024_graphassortativity, author="Wolfram Research", title="{GraphAssortativity}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphAssortativity.html}", note=[Accessed: 25-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_graphassortativity, organization={Wolfram Research}, title={GraphAssortativity}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphAssortativity.html}, note=[Accessed: 25-November-2024 ]}