GraphDiameter

GraphDiameter[g]

gives the greatest distance between any pair of vertices in the graph g.

GraphDiameter[{vw,…}]

uses rules vw to specify the graph g.

Details and Options

  • The following options can be given:
  • EdgeWeightAutomaticweight for each edge
    MethodAutomaticmethod to use
  • With the default setting EdgeWeight->Automatic, the edge weight of an edge is taken to be the EdgeWeight of the graph g if available; otherwise, it is 1.
  • Possible Method settings include "Dijkstra", "FloydWarshall", "Johnson", and "PseudoDiameter".
  • GraphDiameter works with undirected graphs, directed graphs, weighted graphs, multigraphs, and mixed graphs.

Examples

open allclose all

Basic Examples  (1)

Give the graph diameter for a complete graph:

Scope  (7)

GraphDiameter works with undirected graphs:

Directed graphs:

Weighted graphs:

Multigraphs:

Mixed graphs:

Use rules to specify the graph:

GraphDiameter works with large graphs:

Applications  (2)

Illustrate the diameter in two Petersen graphs:

For a CompleteGraph, the diameter is 1:

For a PathGraph of size , the diameter is :

For a CycleGraph of size , the diameter is TemplateBox[{{n, /, 2}}, Floor]:

For a WheelGraph of size 5 or more, the diameter is 2:

A WheelGraph of size 4 is a complete graph, so the diameter is 1:

For a GridGraph of size {m,n}, the diameter is :

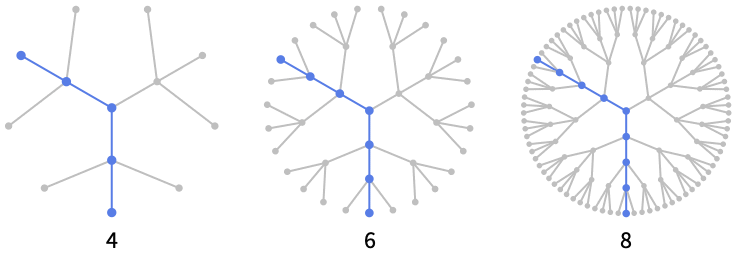
For a CompleteKaryTree tree of depth , the diameter is :

Find the largest number of steps separating two people at a family gathering network:

Properties & Relations  (3)

For a connected graph, the diameter can be computed by VertexEccentricity:

If a simple graph has diameter greater than 3, then its complement has diameter less than 3:

The graph diameter is unchanged when reversing every edge:

Wolfram Research (2010), GraphDiameter, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphDiameter.html (updated 2015).

Text

Wolfram Research (2010), GraphDiameter, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphDiameter.html (updated 2015).

CMS

Wolfram Language. 2010. "GraphDiameter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphDiameter.html.

APA

Wolfram Language. (2010). GraphDiameter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphDiameter.html

BibTeX

@misc{reference.wolfram_2024_graphdiameter, author="Wolfram Research", title="{GraphDiameter}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphDiameter.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_graphdiameter, organization={Wolfram Research}, title={GraphDiameter}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphDiameter.html}, note=[Accessed: 22-December-2024 ]}