GraphUnion

GraphUnion[g1,g2]

给出图 g1 和 g2 的图并集.

GraphUnion[g1,g2,…]

给出图 g1、g2、… 的图并集.

GraphUnion[{vw,…},…]

使用规则 vw 来指定图 g.

更多信息和选项

  • 图的并集 Graph[v1,e1]⋃Graph[v2,e2] 由 Graph[v1⋃v2,e1⋃e2] 给出.
  • GraphUnion 可用于无向图、有向图、多重图和混合图.

背景

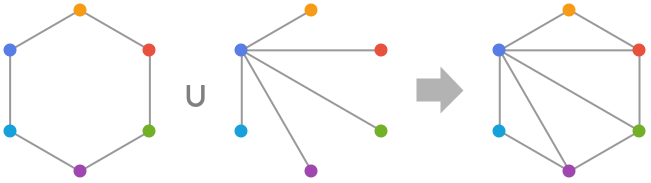
  • GraphUnion 根据两个或更多个有向或无向图得到一个新图，新图的顶点集和边集分别是原先那些图的顶点集的并集和边集的并集. 对不同图中有相同顶点标识的边，GraphUnion 只保留其中一条. 所得的图的边具有原先的顶点标识，且这样标识的边只有一份.
  • 相关函数包括 GraphDisjointUnion、GraphIntersection 和 GraphDifference. 和 GraphUnion 不同，GraphDisjointUnion 保留了全部的边，即使在不同的图中存在多条有相同顶点标识的边. 对 GraphIntersection 给出的图，其顶点集是原先那些图的顶点集的并集，边集是原先那些图的边集的交集. 对 GraphDifference 给出的图，其顶点集是原先那些图的顶点集的并集，边集是第二个图相对于第一个图的补集. 对 GraphComplement 给出的图，其顶点集和原先的图相同但它的边集则是由原先图缺失的那些边构成（反之也成立）.

范例

打开所有单元关闭所有单元

基本范例  (1)

得到两个图的图并集：

突出显示图并集：

范围  (6)

GraphUnion 可用于无向图：

有向图：

多重图：

混合图：

使用规则来指定图：

GraphUnion 可用于超过两个的图：

属性和关系  (7)

图并集的顶点是这些图的顶点的并集：

图并集的边是这些图的边的并集：

一个图和它的子图的并集与它自身同构：

任意简单图和它的补图的并集是一个完全图：

两个图的 GraphUnion 含有和 GraphDifference 相同的顶点：

两个图的 GraphUnion 含有和 GraphIntersection 相同的顶点：

可以使用 GraphUnion 得到 GraphDisjointUnion：

Wolfram Research (2010)，GraphUnion，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GraphUnion.html （更新于 2015 年）.

文本

Wolfram Research (2010)，GraphUnion，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GraphUnion.html （更新于 2015 年）.

CMS

Wolfram 语言. 2010. "GraphUnion." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/GraphUnion.html.

APA

Wolfram 语言. (2010). GraphUnion. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GraphUnion.html 年

BibTeX

@misc{reference.wolfram_2024_graphunion, author="Wolfram Research", title="{GraphUnion}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphUnion.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_graphunion, organization={Wolfram Research}, title={GraphUnion}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphUnion.html}, note=[Accessed: 22-November-2024 ]}