HankelTransform
HankelTransform[expr,r,s]
expr について次数0のHankel変換を与える.
HankelTransform[expr,r,s,ν]
expr について次数 ν のHankel変換を与える.
詳細とオプション

- 関数
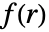 についての次数 ν のHankel変換は
についての次数 ν のHankel変換は ![int_0^inftyr f(r) TemplateBox[{v, {r, , s}}, BesselJ]dr int_0^inftyr f(r) TemplateBox[{v, {r, , s}}, BesselJ]dr](Files/HankelTransform.ja/2.png) と定義される.
と定義される. - Hankel変換は,
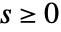 かつ
かつ 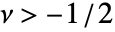 について定義される.
について定義される. - 次は使用可能なオプションである.
-
Assumptions $Assumptions パラメータについての仮定 GenerateConditions False パラメータについての条件を含む結果を生成するかどうか Method Automatic 使用するメソッド - TraditionalFormでは,HankelTransformは
![TemplateBox[{{f, (, r, )}, r, s, nu}, HankelTransform] TemplateBox[{{f, (, r, )}, r, s, nu}, HankelTransform]](Files/HankelTransform.ja/5.png) と出力される.
と出力される.
例題
すべて開くすべて閉じるスコープ (16)
基本的な用法 (5)
記号パラメータ s について関数のHankel変換を計算する:
TraditionalFormで表示する:
オプション (2)
アプリケーション (3)
平面上の放射対称関数のフーリエ(Fourier)変換は,Hankel変換として表すことができる.以下で定義される関数について,この関係を確かめる:
HankelTransformを使って同じ結果を得る:
放射対称関数のリストについて,フーリエ変換の一覧を生成する:
HankelTransformをこの方程式に適用する:
InverseHankelTransformを適用して特殊解を得る:
特性と関係 (6)
Asymptoticを使って漸近近似を計算する:
HankelTransformは積分 ![]() を計算する:
を計算する:
HankelTransformはそれ自身の逆である:
HankelTransformは線形演算子である:
テキスト
Wolfram Research (2017), HankelTransform, Wolfram言語関数, https://reference.wolfram.com/language/ref/HankelTransform.html.
CMS
Wolfram Language. 2017. "HankelTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HankelTransform.html.
APA
Wolfram Language. (2017). HankelTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HankelTransform.html