





Integrate 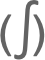
Details and Options


- Integrate[f,x] can be entered as ∫fx.
- ∫ can be entered as
 int
int or \[Integral].
or \[Integral]. - is not an ordinary d; it is entered as
 dd
dd or \[DifferentialD].
or \[DifferentialD]. - Integrate[f,{x,y,…}∈reg] can be entered as ∫{x,y,…}∈regf.
- Integrate[f,{x,xmin,xmax}] can be entered with xmin as a subscript and xmax as a superscript to ∫.
- Multiple integrals use a variant of the standard iterator notation. The first variable given corresponds to the outermost integral and is done last. »
- Integrate can evaluate integrals of rational functions. It can also evaluate integrals that involve exponential, logarithmic, trigonometric, and inverse trigonometric functions, so long as the result comes out in terms of the same set of functions.
- Integrate can give results in terms of many special functions.
- Integrate carries out some simplifications on integrals it cannot explicitly do.
- You can get a numerical result by applying N to a definite integral. »
- You can assign values to patterns involving Integrate to give results for new classes of integrals.
- The integration variable can be a construct such as x[i] or any expression whose head is not a mathematical function.
- For indefinite integrals, Integrate tries to find results that are correct for almost all values of parameters.
- For definite integrals, the following options can be given:
-
Assumptions $Assumptions assumptions to make about parameters GenerateConditions Automatic whether to generate answers that involve conditions on parameters GeneratedParameters None how to name generated parameters PrincipalValue False whether to find Cauchy principal values - Integrate can evaluate essentially all indefinite integrals and most definite integrals listed in standard books of tables.
- In StandardForm, Integrate[f,x] is output as ∫fx.
Examples
open all close allBasic Examples (4)
Scope (78)
Basic Uses (13)
Compute an indefinite integral:
Verify the answer by differentiation:
Use ![]() intt
intt![]() to enter a template
to enter a template ![]() and
and ![]() to move between fields:
to move between fields:
Include the constant of integration in an indefinite integral:
Compute a definite integral over a finite interval:
Use ![]() dintt
dintt![]() to enter a template
to enter a template ![]() and
and ![]() to move between fields:
to move between fields:
Integrate a function with a symbolic parameter:
An integral that only converges for some values of parameters:
Specify alternate assumptions to use:
Multiple integral with x integration last:
In StandardForm, the differential y precedes x:
Visualize the function over the domain of integration:
Integrals over standard regions:
The character ∈ can be entered as ![]() el
el![]() or \[Element]:
or \[Element]:
Enter a region specification ![]() in an underscript using
in an underscript using ![]() :
:
Use ![]() rintt
rintt![]() to enter a template
to enter a template ![]() and
and ![]() to move between fields:
to move between fields:
Integrals of vector- and array-valued functions:
Invoke NIntegrate automatically if symbolic integration fails:
Indefinite Integrals (10)
Generate an answer with a constant of integration:
Integrals of trigonometric functions:
Verify the previous answer via differentiation:
Create a nicely formatted table of integrals:
Rational functions can always be integrated in closed form:
Sometimes they involve sums of Root objects:
Integrals of general elementary functions:
Integrate returns antiderivatives valid in the complex plane where applicable:
A common antiderivative found in integral tables for ![]() is
is ![]() :
:
This is a valid antiderivative for real values of ![]() :
:
On the real line, the two integrals have the same real part:
But the imaginary parts differ by ![]() on any interval where
on any interval where ![]() is negative:
is negative:
Similar integrals can lead to functions of different kinds:
Many integrals can be done only in terms of special functions such as Erf:
Generalizations of Log such as PolyLog and LogIntegral:
Hypergeometric functions such as Hypergeometric2F1:
Create a nicely-formatted table of special function integrals:
Definite Integrals (13)
Visualize the area under the curve:
Integrate a symbolic polynomial:
Integrate over a symbolic range:
Exponential and logarithmic functions:
Hyperbolic trigonometric functions:
Integrate a function with a vertical asymptote:
This can be viewed as a limit of the result of integration on a smaller interval:
Compute the integral of a function with two vertical asymptotes:
This can be viewed as a multivariate limit of the result of integration on a smaller interval:
Integrals over infinite intervals can be viewed as limits of integrals over finite domains:
The preceding is the limit as ![]() of the integral from
of the integral from ![]() to
to ![]() :
:
It is the bivariate limit of a finite integral:
When there are parameters, conditions that ensure convergence may be reported:
Integrals of elementary functions may produce special function answers:
Create a formatted table of definite integrals over the positive reals of special functions:
Integral along a complex line:
Integrate along a piecewise linear contour in the complex plane:
Integrals of Piecewise and Generalized Functions (12)
Compute the indefinite integral of a Piecewise function:
In this case, the derivative of the integral equals the original function:
Integrate a discontinuous Piecewise function:
Except at the point of discontinuity, the derivative of g equals f:
Visualize the function and its antiderivative:
Integrate functions that are piecewise-defined:
Integrate a piecewise function with infinitely many cases:
Everywhere it is defined, the derivative of maxInt equals the original function:
However, maxInt itself is discontinuous:
Compute a definite integral of a Piecewise function:
Compute the integral with a variable endpoint:
Visualize the function and its integral:
Compute definite integrals of piecewise functions such as Floor:
A composition of piecewise functions:
Compute the definite integral with a variable upper limit:
A function with an infinite number of cases:
Integrate over a finite number of cases using Assumptions:
The integral is a continuous function of the upper limit over the domain of integration:
Integrate generalized functions:
Indefinite integrals of generalized functions return generalized functions:
Integrate generalized functions over subsets of the reals:
Integrate an interpolating function:
Nested Integrals (12)
Compute a second antiderivative of a function:
Compute the third antiderivative:
Integrate a function with respect to two different variables:
The mixed partial derivative gives the original function:
Generate a constant of integration for a single integral:
Generate constants for a nested integral with respect to the same variable:
This is the most general second antiderivative of the integrand:
Generate two functions of integration for a nested integral with respect to two variables:
This is the most general mixed antiderivative of the integrand:
Integrate over the rectangle from ![]() to
to ![]() :
:
Integrate in the opposite order:
Combine indefinite and definite integration:
Compute a rational double integral over a rectangular region:
This gives the volume of the shaded region:
Compute a trigonometric double integral over a rectangular region:
There is as much positive volume (dark gray) as negative (light blue):
Compute a polynomial double integral over the area between two curves:
Visualize the domain of integration and the volume corresponding to the integral:
Compute a triple integral over a rectangular prism:
Visualize the region of integration:
Compute an algebraic triple integral over a cone-shaped 3D region:
Visualize the region of integration:
Integrate a multivariate function over a five-dimensional cube:
Integrate ![]() over the unit ball in 4 dimensions:
over the unit ball in 4 dimensions:
Look up the coordinate ranges for hyperspherical coordinates in CoordinateChartData:
Region Integrals (11)
Integrate a constant over a unit disk:
Enter the integral in typeset form:
Equivalently, integrate over a rectangular region and restrict to a disk using Boole:
The same integral expressed using Boole:
The same integral reduced to an iterated integral with bounds depending on the previous variables:
Plot the integrand over the integration region:
Express a normal definite integral using region notation:
Compare with the list notation:
With GenerateConditions True, assumptions are generated so that the region is non-degenerate:
Compare with an iterated integral:
Integrate over the unit circle:
Express the same integral as a one-dimensional integral using polar coordinates:
Integrate over a sphere of radius ![]() :
:
Integrate over a finite set of points:
Regions can be given as logical combinations of inequalities:
Define the region as an ImplicitRegion and integrate directly over the region:
Visualize the domain of integration:
Integral over a three-dimensional region defined by inequalities:
Visualize 3D regions using RegionPlot3D:
Visualize the domain of integration:
Integrate a function with parameters, getting a piecewise result:
Symbolic Features of Integrals (7)
Integrals involving unknown functions are done when possible:
Differentiate with respect to an endpoint, yielding the fundamental theorem of calculus:
Symbolic integrals can be differentiated with respect to parameters:
Differentiate with respect to a parameter that appears in both integrand and endpoints:
Use the Inactive form of Integrate:
Illustrate indefinite integral identities:
Verify the identities starting from the inactive forms:
Illustrate the basic commutation trick for differentiating under the integral sign:
Compute the LaplaceTransform of an integral:
Options (11)
Assumptions (3)
By default, conditions are generated on parameters that guarantee convergence:
With Assumptions, a result valid under the given assumptions is given:
Manually specify Assumptions to test values outside the automatically generated conditions:
This integral is also convergent for purely imaginary ![]() :
:
Specify assumptions to evaluate a piecewise indefinite integral:
GenerateConditions (2)
By default, univariate definite integrals generate conditions on parameters that ensure convergence:
Generate a result without conditions:
Use GenerateConditions->False to speed up integration:
GeneratedParameters (4)
By default a particular antiderivative is returned:
Specify a value of GeneratedParameters to obtain the general antiderivative:
One parameter is generated for each indefinite integral:
If the input expression already contains a generated parameter, the next available index will be used:
For nested integrals with multiple variables, the antiderivative contains arbitrary functions:
This is the most general antiderivative of the integrand:
The value of GeneratedParameters is applied to the index of each generated parameter:
The value can be a pure function:
A value of None disables generated parameters:
Applications (67)
The Geometry of Integrals (5)
The integral ![]() of a constant function
of a constant function ![]() is the signed area of the rectangle of height
is the signed area of the rectangle of height ![]() and width
and width ![]() :
:
The integral ![]() of a piecewise-constant function is the sum of the signed areas of the rectangles defined by its plot:
of a piecewise-constant function is the sum of the signed areas of the rectangles defined by its plot:
The integral ![]() of a general function is the signed area between its plot and the horizontal axis:
of a general function is the signed area between its plot and the horizontal axis:
This can be related to the piecewise-constant case by considering rectangles defined by its plot:
For n5 on the interval [0,2], the rectangles are the following:
The area of these rectangles defines a Riemann sum that approximates the area under the curve:
Using DiscreteLimit to obtain the exact answer as ![]() gives the same answer as Integrate did:
gives the same answer as Integrate did:
Visualize the process for this function as well as three others:
The Fundamental Theorem of Calculus relates a function to its integral from a fixed lower limit to a variable upper limit:
Consider the definite integral of the this from from ![]() to
to ![]() :
:
The Fundamental Theorem of Calculus states that ![]() :
:
This can be seen from the limit definition of derivative:
Note that ![]() is an area consisting of a rectangle of height
is an area consisting of a rectangle of height ![]() and width
and width ![]() plus a small correction that vanishes as
plus a small correction that vanishes as ![]() , as illustrated by the following table for
, as illustrated by the following table for ![]() :
:
Hence, the limit can be seen geometrically to equal ![]() , as illustrated in the following visualization:
, as illustrated in the following visualization:
Integrate a discrete set of data with Interpolation:
Compare with the exact area under the curved that was interpolated:
Area Between Curves (7)
Compute the area under the curve of ![]() from
from ![]() to
to ![]() :
:
Find the area under the curve of ![]() from
from ![]() to
to ![]() :
:
Determine the total area enclosed between of ![]() and the
and the ![]() -axis:
-axis:
The total area is given by the integral of the absolute value:
Equivalently compute this as the sum of two integrals of the difference between the top and bottom:
Compute the area between ![]() and
and ![]() from
from ![]() to
to ![]() :
:
Find the area enclosed by ![]() and
and ![]() :
:
Since ![]() ,
, ![]() will be above
will be above ![]() in the interval of interest and the area will equal:
in the interval of interest and the area will equal:
Visualize the region of interest and the two functions:
Compute the area enclosed by ![]() and
and ![]() :
:
Find the area as the integral of the absolute value of the difference over the entire interval:
Visualize the two functions and the area between them:
Use the plot to split the integral into two equivalent integrals with no absolute value:
To compute the area enclosed by ![]() ,
, ![]() , and
, and ![]() , first find the points of intersection:
, first find the points of intersection:
Visualize the three curves over an area containing the points:
From the plot, it is clear ![]() is above the line
is above the line ![]() and below the other two curves:
and below the other two curves:
Area can be found using two integrals, one for each "top function":
This can be reduced to a single integral using Min:
Compare with the answer returned by Area:
Regions of Revolution (7)
Compute the volume enclosed when ![]() for
for ![]() is rotated about the
is rotated about the ![]() -axis:
-axis:
Use cylindrical shells to find the volume enclosed when ![]() ,
, ![]() , is rotated about the
, is rotated about the ![]() -axis:
-axis:
Visualize the solid, adding the cap at ![]() :
:
Find the volume of the region formed by rotating the area between ![]() and
and ![]() about the
about the ![]() -axis:
-axis:
Find where the curves intersect:
Between these two values of ![]() ,
, ![]() is above
is above ![]() :
:
Integrate cylindrical shells of height ![]() and circumference
and circumference ![]() to find the volume:
to find the volume:
Determine the volume the region above ![]() and below
and below ![]() for
for ![]() , rotated about the
, rotated about the ![]() -axis:
-axis:
Find where the curves intersect, adding the constraint on the range of ![]() :
:
The relevant range of ![]() values is between these two points:
values is between these two points:
Integrate washers of area ![]() to find the volume:
to find the volume:
Compute the surface area when ![]() for
for ![]() is rotated about the
is rotated about the ![]() -axis:
-axis:
Apply the formula of the infinitesimal width of each strip:
Multiply the width by the circumference ![]() of each circle and integrate:
of each circle and integrate:
Find the area when ![]() for -
for -![]() is rotated about the
is rotated about the ![]() -axis:
-axis:
The infinitesimal width of each strip is given by the following:
Multiplying the width by the circumference ![]() and integrating yields the answer:
and integrating yields the answer:
Determine the surface area when ![]() for
for ![]() is rotated about line
is rotated about line ![]() :
:
The infinitesimal width of each strip is given by the following:
Since ![]() for the curve in question, each strip has radius
for the curve in question, each strip has radius ![]() and width
and width ![]() :
:
Find the numerical approximation of this value:
Visualize the surface using modified cylindrical coordinates based on the line ![]() ,
, ![]() :
:
Arc Length, Surface Area, and Volume (8)
Compute the arc length of the plot ![]() from
from ![]() to
to ![]() :
:
Apply the formula for infinitesimal arc length:
Integrate to find the arc length:
Compare with the answer returned by ArcLength:
Compute the arc length of the plot ![]() from
from ![]() to
to ![]() :
:
Apply the formula for infinitesimal arc length:
Integrate to find the arc length:
Compare with the answer returned by ArcLength:
Length of a parametrically defined circle:
The relevant parameter range is ![]() to
to ![]() :
:
The infinitesimal arc length is constant:
Integrate to find the total arc length:
Compare with the answer returned by ArcLength:
Length of a 3D parametrically defined ellipse:
The infinitesimal arc length is non-constant:
Integrate to find the total arc length:
Compare with the answer returned by ArcLength:
Find the surface area of the plot ![]() over the rectangle
over the rectangle ![]() :
:
Apply the formula for infinitesimal surface area of a plot:
Integrate to find the arc length:
Compare with the answer returned by Area:
Find the area of the surface ![]() where
where ![]() :
:
Apply the formula for infinitesimal surface area of a parametric surface:
Integrate to find the total surface area:
Compare with the answer returned by Area:
Find the volume of the following parametric region, where ![]() ,
, ![]() :
:
Compute the Jacobian determinant:
Compare with the answer returned by Volume:
Find the volume of the following parametric region, where ![]() ,
, ![]() , and
, and ![]() :
:
Compute the Jacobian determinant:
Compare with the answer returned by Volume:
Line Integrals (6)
Compute the line integral ![]() of
of ![]() over the origin-centered ellipse with semi-major axes
over the origin-centered ellipse with semi-major axes ![]() and
and ![]() :
:
Perform the integral using the fact that ![]() :
:
Compare the direct integral over the ellipse:
Calculate the closed line integral ![]() of
of ![]() over the following parametric curve:
over the following parametric curve:
The curve forms an infinity figure, traversed from red to purple as shown in the following plot:
Perform the calculation using the definition ![]() :
:
To calculate ∫x4dx+x yy over the triangle with vertices ![]() ,
, ![]() , and
, and ![]() , define the associated vector field:
, define the associated vector field:
Parametrize the triangle using a piecewise-linear parametrization:
The parametrization is oriented counter-clockwise:
Compute the line integral from the definition ![]() :
:
Calculate the work done by the force ![]() as a particle takes the following path from
as a particle takes the following path from ![]() ,
, ![]() , to
, to ![]() ,
, ![]() :
:
Define the force field as function from points to vectors:
The work done is the line integral ![]() :
:
Find a potential function for the following vector field:
This is possible because the vector field is conservative:
Define a family of straight-line curves that go from the origin at time ![]() to
to ![]() at time
at time ![]() :
:
Let ![]() be the line integral of
be the line integral of ![]() from the origin to the point
from the origin to the point ![]() :
:
Verify that ![]() is a potential function for
is a potential function for ![]() using Grad
using Grad
Use Green's Theorem to find the area of the area enclosed by the following curve:
The following vector-field has a two-dimensional Curl of ![]() :
:
Surface and Volume Integrals (7)
Use Green's Theorem to compute ![]() over the circle centered at the origin with radius 3:
over the circle centered at the origin with radius 3:
Visualize the vector field and circle for the line integral:
The circulation of the vector field can be computed using Curl:
Integrate over the interior of the circle:
Perform the integral using region notation:
Compute the integral over the unit sphere of ![]() :
:
Determine infinitesimal surface area:
Compare with a region integral:
Verify Stoke's theorem for ![]() for the upper unit hemisphere:
for the upper unit hemisphere:
Parameterize the surface using standard spherical coordinates:
Visualize the surface and the vector field:
The boundary of the surface is the unit circle in the ![]() -plane:
-plane:
Compute the curl of the vector field:
Compute the oriented surface area element on the hemisphere:
Stoke's theorem, ![]() , states that line integral of
, states that line integral of ![]() on boundary equals the flux integral of its curl through the surface:
on boundary equals the flux integral of its curl through the surface:
Use the divergence theorem to compute the flux of ![]() through the surface bounded above by
through the surface bounded above by ![]() , below by
, below by ![]() , and on the side by
, and on the side by ![]() and
and ![]() :
:
The divergence theorem, ![]() , relates the flux to the volume integral of the divergence:
, relates the flux to the volume integral of the divergence:
Use Gauss's Theorem to find the volume enclosed by the following parametric surface:
The oriented area element on the surface is given by the following:
The following vector-field has a divergence equal ![]() :
:
Apply Gauss's Theorem in the form![]() to compute the volume:
to compute the volume:
Given a mass density ![]() , find the mass of region given by the following:
, find the mass of region given by the following:
The ranges of the parameters are ![]() and
and ![]() , producing a filled torus:
, producing a filled torus:
Enter the mass density function:
Compute the Jacobian determinate:
Integrate to find the total mass:
Derive a formula for the integral of ![]() over an
over an ![]() -dimensional unit ball:
-dimensional unit ball:
Average Values and Centroids (6)
Compute the average value of ![]() between
between ![]() and
and ![]() :
:
Visualize the function and its average value:
Find the mean of ![]() over the parallelogram based at the origin with sides
over the parallelogram based at the origin with sides ![]() and
and ![]() :
:
As ![]() , the mean is given by the following ratio of integrals:
, the mean is given by the following ratio of integrals:
Express the integrals using region notation:
Visualize the function and its mean value:
To compute the centroid of the region under the curve of ![]() from
from ![]() to
to ![]() , first find the area:
, first find the area:
The centroid equals the average value of the coordinates:
Compare with the answer given by RegionCentroid:
Determine the centroid of the region between the curves ![]() and
and ![]() from
from ![]() to
to ![]() :
:
Compare with the answer returned by RegionCentroid:
Visualize the region and its centroid:
Derive general formulas for the centroid of the region under the curve ![]() from
from ![]() to
to ![]() using the fact that the integral gives the area under the curve:
using the fact that the integral gives the area under the curve:
The ![]() centroid is the mean value of
centroid is the mean value of ![]() over the region from
over the region from ![]() to
to ![]() and from
and from ![]() to
to ![]() :
:
The ![]() centroid is similarly the mean value of
centroid is similarly the mean value of ![]() :
:
Find the center of mass of the origin-centered hemisphere of radius ![]() with
with ![]() :
:
First compute the volume of the region:
The center of mass is the average value of the position vector:
Probability, Expectation, and Standard Deviation (7)
Compute the probability that ![]() when
when ![]() follows a standard normal distribution:
follows a standard normal distribution:
Compare with the value returned by Probability:
Compute the probability that ![]() for an exponential distribution with mean
for an exponential distribution with mean ![]() . The mean is the reciprocal of the parameter:
. The mean is the reciprocal of the parameter:
Thus, use the probability density function (PDF) for ExponentialDistribution[5/2]:
Since the PDF vanishes for ![]() , the probability that
, the probability that ![]() is the integral from
is the integral from ![]() to
to ![]() :
:
The corresponding probabilistic statements:
Compute the probability that a value is within two standard deviations of the mean in a normal distribution:
Compare with the answer returned by Probability:
This can be interpreted as saying that about ![]() of the entire area under the curve lies between
of the entire area under the curve lies between ![]() and
and ![]() in the following plot:
in the following plot:
Compute the expectation of ![]() when
when ![]() follows a standard Cauchy distribution:
follows a standard Cauchy distribution:
Compare with the answer returned by Expectation:
Mean and variance of the normal distribution:
Compare with the built in functions Mean and Variance:
Show that the standard deviation of an exponential distribution with mean μ is also μ:
Compare with the answers returned by Mean and StandardDeviation:
Compute the cumulative distribution function (CDF) from the probability density function (PDF):
Integral Transforms (7)
Compare with FourierTransform:
Compare with LaplaceTransform:
Since the function is even, the Hartley transform is equivalent to FourierCosTransform:
Find the Fourier coefficients of a function on [0,1]:
Define the partial sums of the transform:
Visualize the partial sums, which exhibit the Gibbs phenomenon due to the aperiodicity of ![]() :
:
Compare with MellinTransform:
Compare with HankelTransform:
Compute a quadratic fractional Fourier transform in closed form:
Visualize the real and imaginary parts of the transform for different values of α:
Real and Complex Analysis (4)
Define the standard ![]() norm of a univariate function:
norm of a univariate function:
Also define a formatting for this function:
Compute the norms as a function of ![]() for three different functions:
for three different functions:
The norm is always eventually an increasing function of ![]() , but it may be initially decreasing:
, but it may be initially decreasing:
The Fourier transform is an ![]() isomorphism (the norm of the function and its transform are equal):
isomorphism (the norm of the function and its transform are equal):
It is not, however, an ![]() isomorphism for any other value, for example for
isomorphism for any other value, for example for ![]() :
:
Define the weighted inner product for ![]() , with weight
, with weight ![]() for functions defined on
for functions defined on ![]() :
:
Orthogonality of Legendre polynomials ![]() on
on ![]() with weight function
with weight function ![]() :
:
Orthogonality of Chebyshev polynomials ![]() on
on ![]() with weight function
with weight function ![]() :
:
Orthogonality of Hermite polynomials ![]() on
on ![]() with weight function
with weight function ![]() :
:
Define an inner product on functions using Integrate:
Construct an orthonormal basis using using Orthogonalize:
This inner product produces the Gegenbauer polynomials:
Compute the residue of ![]() at
at ![]() as an integral over a contour enclosing
as an integral over a contour enclosing ![]() :
:
Compare with the answers returned by Residue:
Properties & Relations (14)
Integration is a linear operator:
Indefinite integration is the inverse of differentiation:
Definite integration can be defined in terms of DiscreteLimit and Sum:
Evaluate integrals numerically using N:
This effectively calls NIntegrate:
Derivative with a negative integer order does integrals:
ArcLength is the integral of 1 over a one-dimensional region:
Area is the integral of 1 over a two-dimensional region:
Volume is the integral of 1 over a three-dimensional region:
RegionMeasure for a region ![]() is given by the integral
is given by the integral ![]() :
:
RegionCentroid is equivalent to Integrate[p,p∈ℛ]/m with m=RegionMeasure[ℛ]:
Solve a simple differential equation:
DSolveValue returns a solution with the constant of integration:
DSolve returns a substitution rule for the solution:
Integrate computes the integral in closed form:
AsymptoticIntegrate gives series approximating the exact result:
FourierTransform is defined in terms of an integral:
LaplaceTransform is defined in terms of an integral:
Possible Issues (13)
Indefinite Integrals (6)
Many simple integrals cannot be evaluated in terms of standard mathematical functions:
The indefinite integral of a continuous function can be discontinuous:
Using a definite integral with a variable upper limit can smooth the discontinuity. Find the discontinuity to the left of the plot:
In this case, integrating from previous discontinuity reproduces the values of the indefinite integral in the range ![]() :
:
The derivative of an integral may not come out in the same form as the original function:
Simplify and related constructs can often show equivalence:
Different forms of the same integrand can give integrals that differ by constants of integration:
Parameters like ![]() are assumed to be generic inside indefinite integrals:
are assumed to be generic inside indefinite integrals:
Use definite integration with a variable upper limit to generate conditions:
When part of a sum cannot be integrated explicitly, the whole sum will stay unintegrated:
Definite Integrals (7)
Substituting limits into an indefinite integral may not give the correct result for a definite integral:
The presence of a discontinuity in the expression for the indefinite integral leads to the anomaly:
Specifying integer assumptions may not give a simpler result:
Use Simplify and related functions to obtain the expected result:
One can specify a real range as an assumption:
Numeric integration agrees with this for n=π:
It happens that this integral does converge on a subset of zero measure, the positive integers:
A discrete subcase specification such as integrality will still give the generic result:
A definite integral may have a closed form only over an infinite interval:
Integrals over regions do not test whether an integrand is absolutely integrable:
Answers may then depend on how the region was decomposed for integration:
Integrals over zero-dimensional regions use the counting measure:
To use the measure of the ambient space, integrate over all space with the added condition ![]() :
:
Setting GenerateConditions to False may produce unexpected answers:
In this case, the condition that the integral is divergent was lost:
Interactive Examples (1)
Consider Gabriel's horn, the interior of rotating ![]() around the
around the ![]() axis for
axis for ![]() :
:
Compute the volume for arbitrary endpoint ![]() :
:
Compute the surface area for arbitrary endpoint ![]() :
:
The limit as ![]() of the volume is finite, but the surface area is infinite:
of the volume is finite, but the surface area is infinite:
Visualize the horn along with its volume and surface area as functions of ![]() :
:
See Also
NIntegrate AsymptoticIntegrate LineIntegrate SurfaceIntegrate ContourIntegrate Asymptotic DSolve Sum LaplaceTransform FourierTransform Convolve D Derivative CDF Expectation Probability ArcLength Area Volume MomentOfInertia FractionalD CaputoD ResidueSum
Characters: \[Integral] \[DifferentialD]
Function Repository: FractionalIntegrate RiemannSum
Related Guides
Related Links
History
Introduced in 1988 (1.0) | Updated in 1996 (3.0) ▪ 2003 (5.0) ▪ 2014 (10.0) ▪ 2019 (12.0)
Text
Wolfram Research (1988), Integrate, Wolfram Language function, https://reference.wolfram.com/language/ref/Integrate.html (updated 2019).
CMS
Wolfram Language. 1988. "Integrate." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Integrate.html.
APA
Wolfram Language. (1988). Integrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Integrate.html
BibTeX
@misc{reference.wolfram_2025_integrate, author="Wolfram Research", title="{Integrate}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Integrate.html}", note=[Accessed: 18-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_integrate, organization={Wolfram Research}, title={Integrate}, year={2019}, url={https://reference.wolfram.com/language/ref/Integrate.html}, note=[Accessed: 18-January-2026]}