HeatRadiationValue
HeatRadiationValue[pred,vars,pars]
represents a thermal radiation boundary condition for PDEs with predicate pred indicating where it applies, with model variables vars and global parameters pars.
HeatRadiationValue[pred,vars,pars,lkey]
represents a thermal radiation boundary condition with local parameters specified in pars[lkey].
Details




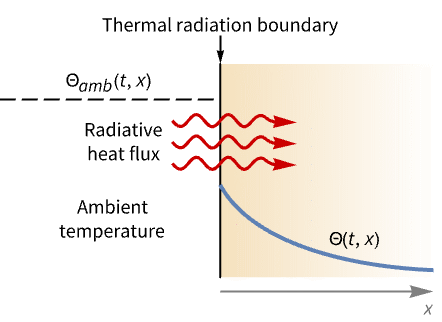
- HeatRadiationValue specifies a boundary condition for HeatTransferPDEComponent and is used as part of the modeling equation:
- HeatRadiationValue is typically used to model heating or cooling through radiation on some part of the boundary. Common examples include an electrical radiator or a fireplace.
- HeatRadiationValue models heating or cooling through radiation with dependent variable
 [
[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/HeatRadiationValue.en/4.png) ], independent variables
], independent variables 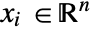 in [
in [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/HeatRadiationValue.en/6.png) ] and time variable
] and time variable 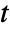 in [
in [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/HeatRadiationValue.en/8.png) ].
]. - Stationary variables vars are vars={Θ[x1,…,xn],{x1,…,xn}}.
- Time-dependent variables vars are vars={Θ[t,x1,…,xn],t,{x1,…,xn}}.
- The non-conservative time-dependent heat transfer model HeatTransferPDEComponent is based on a convection-diffusion model with mass density
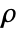 , specific heat capacity
, specific heat capacity 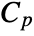 , thermal conductivity
, thermal conductivity 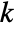 , convection velocity vector
, convection velocity vector 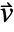 and heat source
and heat source 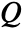 :
: - The thermal radiation value HeatRadiationValue with
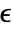 the dimensionless emissivity,
the dimensionless emissivity, 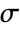 the Boltzmann constant,
the Boltzmann constant, 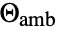 an ambient temperature and
an ambient temperature and 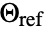 a reference temperature and boundary unit normal
a reference temperature and boundary unit normal 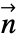 models:
models: - The emissivity
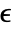 is the effectiveness of a material emitting heat and can have a value in the range of
is the effectiveness of a material emitting heat and can have a value in the range of 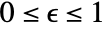 .
. - Model parameters pars as specified for HeatTransferPDEComponent.
- The following additional model parameters pars can be given:
-
parameter default symbol "AmbientTemperature" - 0
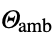 , ambient temperature [
, ambient temperature [![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/HeatRadiationValue.en/25.png) ]
]"BoltzmannConstant" 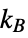
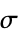 , Boltzmann constant [
, Boltzmann constant [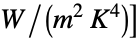
"Emissivity" 1 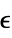
"ReferenceTemperature" 0 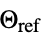 , reference temperature [
, reference temperature [![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/HeatRadiationValue.en/31.png) ]
] - The Boltzmann constant has units [
 ] and the temperatures of the PDE model need to be specified in Kelvin.
] and the temperatures of the PDE model need to be specified in Kelvin. - The "BoltzmannConstant" parameter can only be specified in pars, not with lkey.
- The default reference temperature is 0 Kelvin, but other units can be used after a conversion.
- The ambient temperature
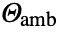 and the reference temperature
and the reference temperature 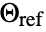 can be nonlinear functions of time
can be nonlinear functions of time 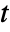 , space
, space 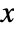 and the dependent variable
and the dependent variable  .
. - To localize model parameters, a key lkey can be specified, and values from association pars[lkey] are used for model parameters.
- All model parameters may depend on any of
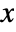 ,
, 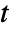 and
and  , as well as other dependent variables.
, as well as other dependent variables. - HeatRadiationValue is a special case of a HeatFluxValue.
- HeatRadiationValue evaluates to a generalized NeumannValue.
- The boundary predicate pred can be specified as in NeumannValue.
- If the HeatRadiationValue depends on parameters
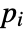 that are specified in the association pars as …,keypi…,pivi,…], the parameters
that are specified in the association pars as …,keypi…,pivi,…], the parameters 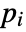 are replaced with
are replaced with 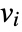 .
.
Examples
open allclose allBasic Examples (2)
Set up a thermal radiation boundary condition:
Model a temperature field and a thermal radiation boundary with:
Set up the heat transfer model variables ![]() :
:
Specify heat transfer model parameters mass density ![]() , specific heat capacity
, specific heat capacity ![]() and thermal conductivity
and thermal conductivity ![]() :
:
Specify boundary condition parameters with a constant ambient temperature ![]() of –25 °C and a surface emissivity
of –25 °C and a surface emissivity ![]() of
of ![]() :
:
Scope (6)
Basic Examples (5)
Define model variables vars for a transient temperature field with model parameters pars and a specific boundary condition parameter:
Define model variables vars for a transient temperature field with model parameters pars and multiple specific parameter boundary conditions:
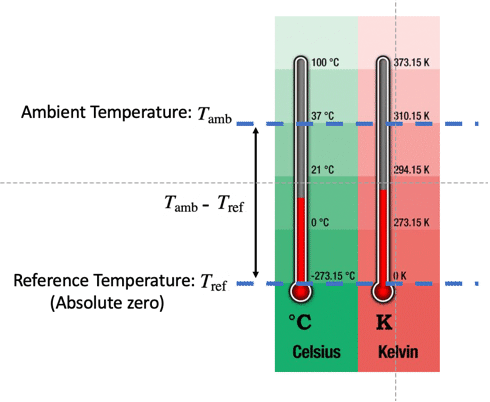
Set up a reference temperature of absolute zero in degrees Celsius:
Set up a thermal radiation boundary condition with a reference and ambient temperature in Celsius:
If no value for emissivity ![]() is specified, then an emissivity of 1 is assumed:
is specified, then an emissivity of 1 is assumed:
Set up a thermal radiation boundary condition with ambient temperature ![]() emissivity
emissivity ![]() :
:
2D (1)
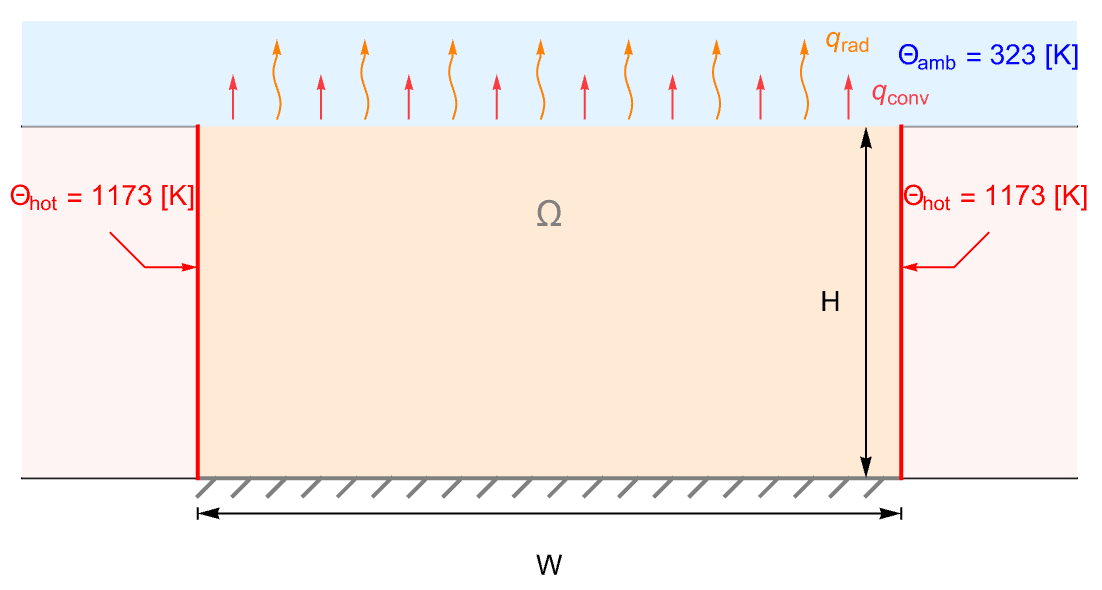
Model a ceramic strip that is embedded in a high-thermal-conductive material. The side boundaries of the strip are maintained at a constant temperature ![]() . The top surface of the strip is losing heat via both heat convection and heat radiation to the ambient environment at
. The top surface of the strip is losing heat via both heat convection and heat radiation to the ambient environment at ![]() . The bottom boundary, however, is assumed to be thermally insulated:
. The bottom boundary, however, is assumed to be thermally insulated:
Model a temperature field and the thermal radiation and thermal transfer with:
Set up the heat transfer model variables ![]() :
:
Set up a rectangular domain with a width of ![]() and a height of
and a height of ![]() :
:
Specify thermal conductivity ![]() :
:
Set up temperature surface boundary conditions ![]() at the left and right boundaries:
at the left and right boundaries:
Set up a heat transfer boundary condition on the top surface:
Also set up a thermal radiation boundary condition on the top surface:
Applications (1)
Model the temperature field and a thermal radiation boundary with:
Set up the heat transfer model variables ![]() :
:
Specify heat transfer model parameters density ![]() , specific heat capacity
, specific heat capacity ![]() and thermal conductivity
and thermal conductivity ![]() :
:
Specify boundary condition parameters with a constant ambient temperature ![]() of
of ![]()
![]() and a surface emissivity
and a surface emissivity ![]() of
of ![]() :
:
Text
Wolfram Research (2020), HeatRadiationValue, Wolfram Language function, https://reference.wolfram.com/language/ref/HeatRadiationValue.html (updated 2022).
CMS
Wolfram Language. 2020. "HeatRadiationValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/HeatRadiationValue.html.
APA
Wolfram Language. (2020). HeatRadiationValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeatRadiationValue.html