HeatRadiationValue
HeatRadiationValue[pred,vars,pars]
偏微分方程式の熱放射境界条件を表す.述語 pred はモデル変数 vars と大域パラメータ pars でこれが適応されるところを示す.
HeatRadiationValue[pred,vars,pars,lkey]
pars[lkey]で指定される局所パラメータで熱放射境界条件を表す.
詳細



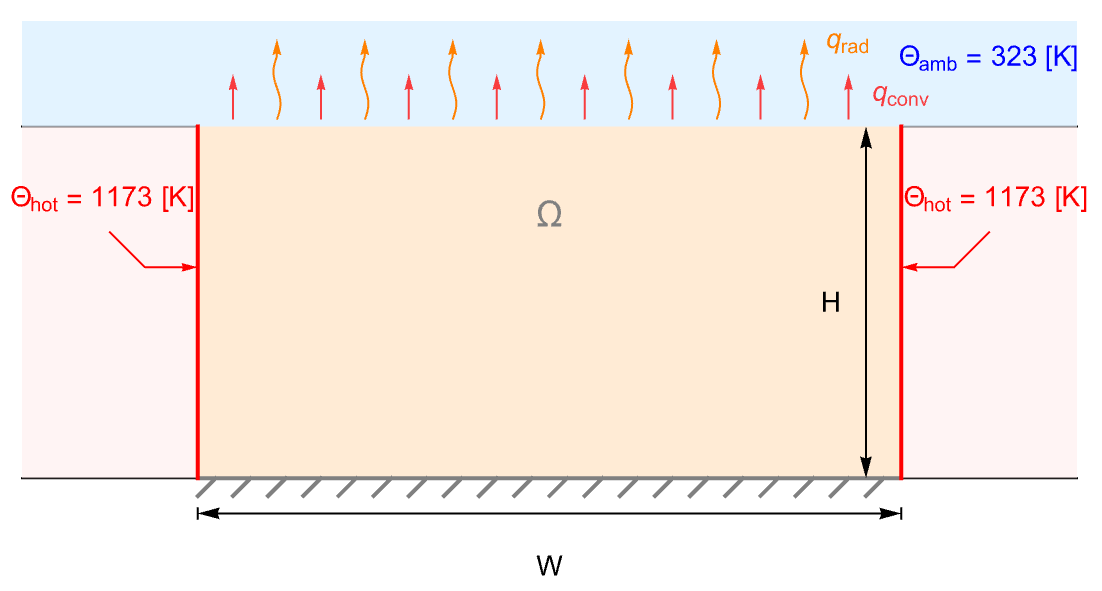
- HeatRadiationValueはHeatTransferPDEComponentの境界条件を指定し,以下のモデリング方程式の一部として使われる.
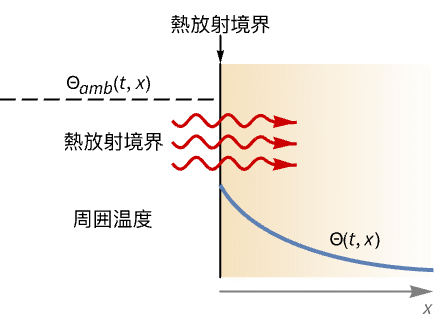
- HeatRadiationValueは,境界の一部からの放射による暖房あるいは冷房のモデル化に使われることが多い.例として電気ラジエータや暖炉が挙げられる.
- HeatRadiationValueは,放射による暖房あるいは冷房を従属変数
 [
[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/HeatRadiationValue.ja/4.png) ],独立変数
],独立変数 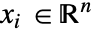 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/HeatRadiationValue.ja/6.png) ]),時間変数
]),時間変数 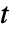 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/HeatRadiationValue.ja/8.png) ])でモデル化する.
])でモデル化する. - 定常変数 vars は vars={Θ[x1,…,xn],{x1,…,xn}}である.
- 時間依存変数 vars は vars={Θ[t,x1,…,xn],t,{x1,…,xn}}である.
- 非保存型時間依存熱移動モデルHeatTransferPDEComponentは,質量密度
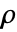 ,比熱容量
,比熱容量 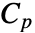 ,熱伝導率
,熱伝導率 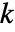 ,対流速度
,対流速度 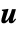 ,熱源
,熱源 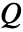 の対流拡散モデルに基づいている.
の対流拡散モデルに基づいている. - 無次元の放射率
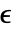 ,ボルツマン定数
,ボルツマン定数 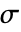 ,周囲温度
,周囲温度 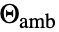 ,基準温度
,基準温度 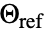 ,境界単位法線
,境界単位法線 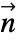 の熱放射値 HeatRadiationValueは以下をモデル化する.
の熱放射値 HeatRadiationValueは以下をモデル化する. - 放射率
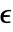 は熱を放射している材料の有効性で値の範囲は
は熱を放射している材料の有効性で値の範囲は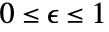 である.Quantity[None,"Wat"] /("Meters"^2*"Kelvins"^4)
である.Quantity[None,"Wat"] /("Meters"^2*"Kelvins"^4) - モデルのパラメータ pars はHeatTransferPDEComponentについてと同じように指定できる.
- 次の追加的なモデルパラメータ pars が使用できる.
-
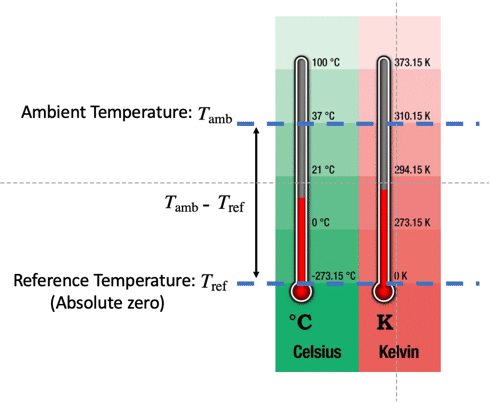
パラメータ デフォルト シンボル "AmbientTemperature" - 0
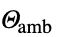 (周辺温度,単位:[
(周辺温度,単位:[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/HeatRadiationValue.ja/25.png) ])
])"BoltzmannConstant" 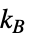
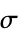 (ボルツマン定数,単位:[
(ボルツマン定数,単位:[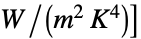 )
)"Emissivity" 1 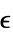
"ReferenceTemperature" 0 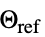 (基準温度,単位:[
(基準温度,単位:[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/HeatRadiationValue.ja/31.png) ])
]) - ボルツマン定数の単位は[
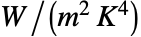 ]で,偏微分方程式モデルの温度はケルビン単位で指定されなければならない.
]で,偏微分方程式モデルの温度はケルビン単位で指定されなければならない. - "BoltzmannConstant"パラメータは pars でのみ指定できる(lkey では指定できない).
- デフォルトの基準温度は0ケルビンだが,変換後に別の単位を使うことができる.
- 周囲温度
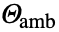 および基準温度
および基準温度 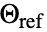 は,時間
は,時間 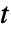 ,空間
,空間 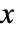 ,従属変数
,従属変数  の非線形関数でよい.
の非線形関数でよい. - モデルのパラメータを局所化したければ,キー lkey を指定するとよい.こうすると,連想からの値 pars[lkey]がモデルのパラメータに使われる.
- モデルパラメータはどれも,
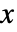 ,
,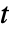 ,
, の任意のものあるいは他の従属変数に依存することがある.
の任意のものあるいは他の従属変数に依存することがある. - HeatRadiationValueはHeatFluxValueの特殊ケースである.
- HeatRadiationValueを評価すると一般化されたNeumannValueになる.
- 境界述語 pred はNeumannValueにおけるのと同じように指定できる.
- HeatRadiationValueが…,keypi…,pivi,…]のように連想 pars の中で指定されるパラメータ
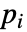 に依存するなら,パラメータ
に依存するなら,パラメータ 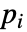 は
は 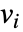 で置換される.
で置換される.
例題
すべて開くすべて閉じる例 (2)
スコープ (6)
基本的な例題 (5)
Wolfram Research (2020), HeatRadiationValue, Wolfram言語関数, https://reference.wolfram.com/language/ref/HeatRadiationValue.html (2022年に更新).
テキスト
Wolfram Research (2020), HeatRadiationValue, Wolfram言語関数, https://reference.wolfram.com/language/ref/HeatRadiationValue.html (2022年に更新).
CMS
Wolfram Language. 2020. "HeatRadiationValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/HeatRadiationValue.html.
APA
Wolfram Language. (2020). HeatRadiationValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeatRadiationValue.html