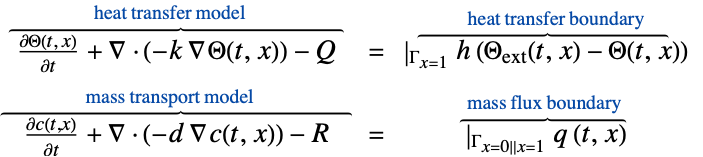HeatTransferPDEComponent[vars,pars]
モデル変数が vars でモデルパラメータが pars の熱移動PDE項を与える.


HeatTransferPDEComponent
HeatTransferPDEComponent[vars,pars]
モデル変数が vars でモデルパラメータが pars の熱移動PDE項を与える.
詳細




- HeatTransferPDEComponentは,微分方程式の一部として使われる微分演算子の和を返す.
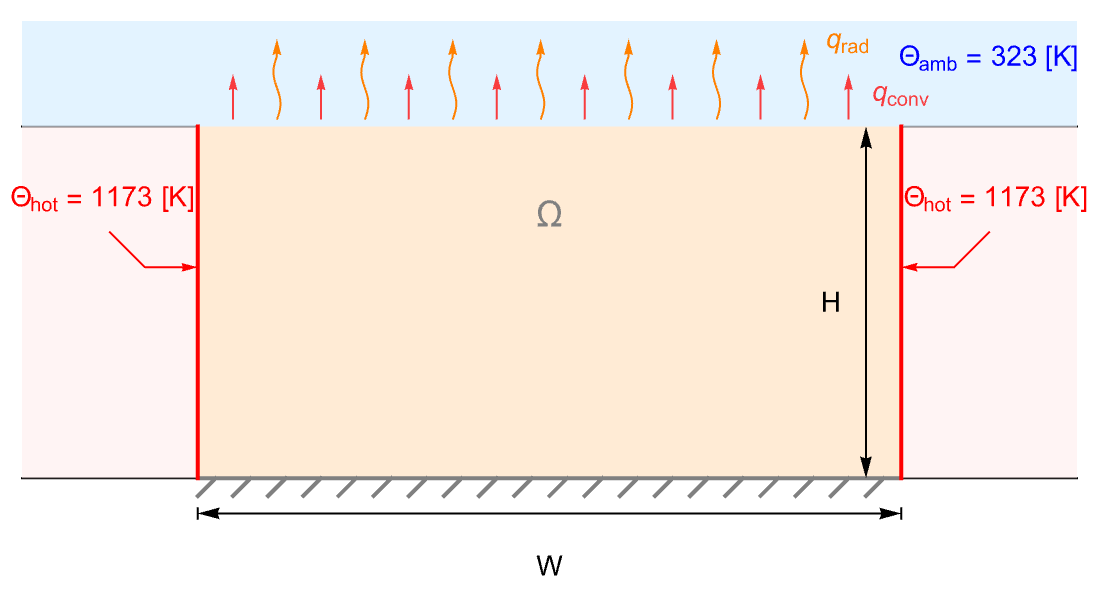
- HeatTransferPDEComponentは,物理系における,対流,伝導,放射等のメカニズムによる,熱エネルギーの生成と伝播をモデル化する.
- HeatTransferPDEComponentは,熱移動現象を,従属変数温度
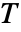 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/HeatTransferPDEComponent.ja/4.png) ]),独立変数
]),独立変数 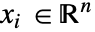 (単位: [
(単位: [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/HeatTransferPDEComponent.ja/6.png) ]),時間変数
]),時間変数 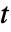 (単位:[
(単位:[![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/HeatTransferPDEComponent.ja/8.png) ])でモデル化する.
])でモデル化する. - 定常変数 vars は vars={Θ[x1,…,xn],{x1,…,xn}}である.
- 時間依存変数 vars は vars={Θ[t,x1,…,xn],t,{x1,…,xn}}である.
- 非保存型時間依存熱移動PDE HeatTransferPDEComponentは,質量密度
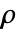 ,比熱容量
,比熱容量 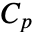 ,熱移動率
,熱移動率 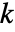 ,対流速度ベクトル
,対流速度ベクトル 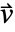 ,熱源
,熱源 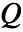 の対流拡散項に基づいている.
の対流拡散項に基づいている. - 非保存型定常熱移動モデルは以下で与えられる.
- 非保存型モデルについての陰的デフォルト境界条件はHeatOutflowValueである:
- 非保存型モデルと保存型モデルの違いは対流速度
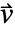 の扱いである.
の扱いである. - 熱移動モデル項の単位は[
![TemplateBox[{InterpretationBox[, 1], {"W", , "/", , {"m", ^, 3}}, watts per meter cubed, {{(, "Watts", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"W", , "/", , {"m", ^, 3}}, watts per meter cubed, {{(, "Watts", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/HeatTransferPDEComponent.ja/17.png) ],つまり,[
],つまり,[![TemplateBox[{InterpretationBox[, 1], {"J", , "/(", , {"m", ^, 3}, , "s", , ")"}, joules per meter cubed second, {{(, "Joules", )}, /, {(, {{"Meters", ^, 3}, , "Seconds"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"J", , "/(", , {"m", ^, 3}, , "s", , ")"}, joules per meter cubed second, {{(, "Joules", )}, /, {(, {{"Meters", ^, 3}, , "Seconds"}, )}}}, QuantityTF]](Files/HeatTransferPDEComponent.ja/18.png) ]と同等である.
]と同等である. - 次のパラメータ pars が使用できる.
-
パラメータ デフォルト シンボル "HeatConvectionVelocity" {0,…} 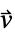 (流速,単位:[
(流速,単位:[![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/HeatTransferPDEComponent.ja/20.png) ])
])"HeatSource" 0 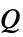 (熱源,単位:[
(熱源,単位:[![TemplateBox[{InterpretationBox[, 1], {"W", , "/", , {"m", ^, 3}}, watts per meter cubed, {{(, "Watts", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"W", , "/", , {"m", ^, 3}}, watts per meter cubed, {{(, "Watts", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/HeatTransferPDEComponent.ja/22.png) ])
])"MassDensity" 1 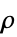 (密度,単位:[
(密度,単位:[![TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/HeatTransferPDEComponent.ja/24.png) ])
])"Material" Automatic 
"ModelForm" "NonConservative" なし "RegionSymmetry" None 
"SpecificHeatCapacity" 1 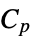 (熱容量,単位:
(熱容量,単位:![TemplateBox[{InterpretationBox[, 1], {"J", , "/(", , "kg", , "K", , ")"}, joules per kilogram kelvin, {{(, "Joules", )}, /, {(, {"Kilograms", , "Kelvins"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"J", , "/(", , "kg", , "K", , ")"}, joules per kilogram kelvin, {{(, "Joules", )}, /, {(, {"Kilograms", , "Kelvins"}, )}}}, QuantityTF]](Files/HeatTransferPDEComponent.ja/28.png) ])
])"ThermalConductivity" IdentityMatrix 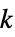 (熱伝導率,単位: [
(熱伝導率,単位: [![TemplateBox[{InterpretationBox[, 1], {"W", , "/(", , "m", , "K", , ")"}, watts per meter kelvin, {{(, "Watts", )}, /, {(, {"Meters", , "Kelvins"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"W", , "/(", , "m", , "K", , ")"}, watts per meter kelvin, {{(, "Watts", )}, /, {(, {"Meters", , "Kelvins"}, )}}}, QuantityTF]](Files/HeatTransferPDEComponent.ja/30.png) ])
]) - パラメータはどれも,任意の
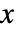 ,
,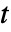 ,
,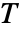 およびその他の従属変数に依存する可能性がある.
およびその他の従属変数に依存する可能性がある. - 独立変数の数
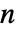 は
は 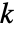 の次元と
の次元と 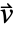 の長さを決定する.
の長さを決定する. - 時に熱伝導方程式が熱拡散率で指定されることがある.熱拡散率は熱伝導率を密度と定圧での比熱容量で割ったものである.
- 熱対流速度は,液体が熱を運ぶ速度
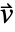 を指定する.液体がない場合は,熱対流速度は0である.
を指定する.液体がない場合は,熱対流速度は0である. - 熱源
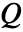 は,系に取り入れられる(正の)あるいは系から取り除かれる(負の)熱エネルギーをモデル化する.
は,系に取り入れられる(正の)あるいは系から取り除かれる(負の)熱エネルギーをモデル化する. - パラメータ"RegionSymmetry"の可能な選択肢には"Axisymmetric"がある.
- "Axisymmetric"領域対称性は,以下のように角度変数を削除することで円柱座標が縮小された切り取られた円柱座標系を表す.
-
次元 縮小 方程式 1D 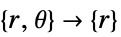
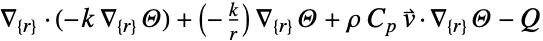
2D 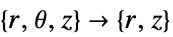
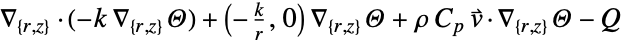
- パラメータの入力指定は対応する演算子項と全く同じである.
- 結合方程式は対応する演算子形と同じ入力指定で生成できる.
- パラメータが指定されていない場合のデフォルトの熱移動PDEは以下になる.
- HeatTransferPDEComponentが…,keypi…,pivi,…のような連想 pars で指定されるパラメータ
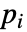 に依存する場合は,パラメータ
に依存する場合は,パラメータ 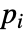 は
は 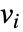 で置換される.
で置換される.

例題
すべて開く すべて閉じる例 (4)
スコープ (7)
1D (1)
2D (1)
3D (1)
時間依存 (1)
アプリケーション (7)
境界条件 (5)
関連するガイド
テキスト
Wolfram Research (2020), HeatTransferPDEComponent, Wolfram言語関数, https://reference.wolfram.com/language/ref/HeatTransferPDEComponent.html (2022年に更新).
CMS
Wolfram Language. 2020. "HeatTransferPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/HeatTransferPDEComponent.html.
APA
Wolfram Language. (2020). HeatTransferPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeatTransferPDEComponent.html
BibTeX
@misc{reference.wolfram_2025_heattransferpdecomponent, author="Wolfram Research", title="{HeatTransferPDEComponent}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/HeatTransferPDEComponent.html}", note=[Accessed: 17-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_heattransferpdecomponent, organization={Wolfram Research}, title={HeatTransferPDEComponent}, year={2022}, url={https://reference.wolfram.com/language/ref/HeatTransferPDEComponent.html}, note=[Accessed: 17-February-2026]}