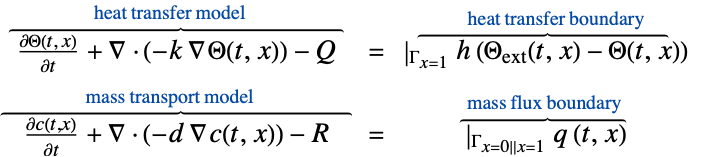HeatTransferValue
HeatTransferValue[pred,vars,pars]
代表偏微分方程的传热边界条件,其中谓词 pred 指示其适用位置,模型变量为 vars,全局参数为 pars.
HeatTransferValue[pred,vars,pars,lkey]
表示局部参数在 pars[lkey] 中指定的传热边界条件.
更多信息
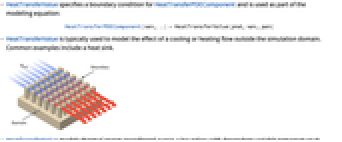

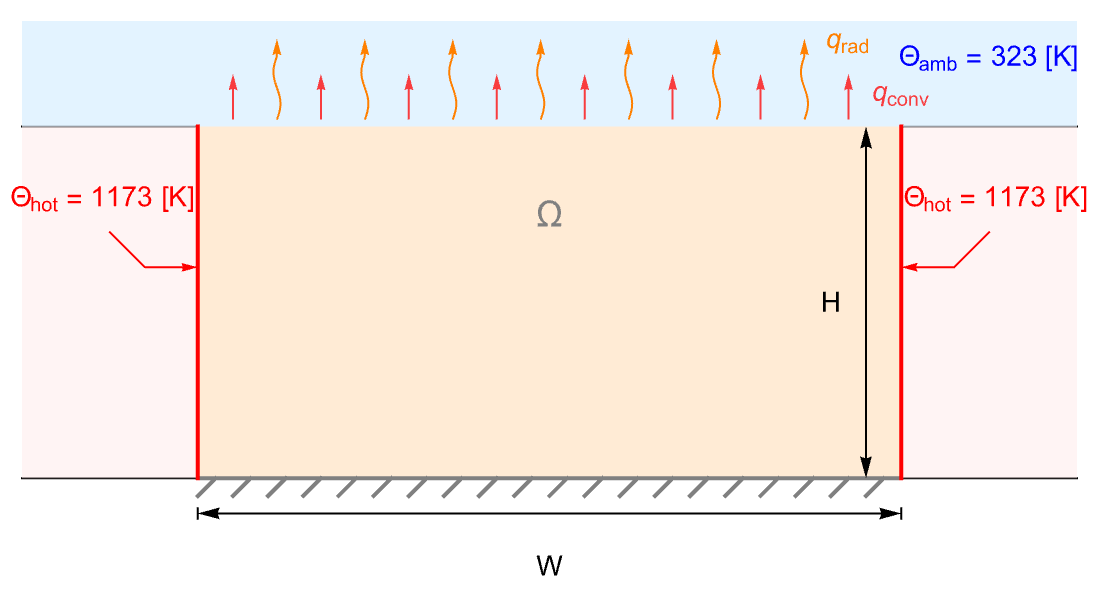
- HeatTransferValue 指定 HeatTransferPDEComponent 的边界条件,并用作以下建模方程式的一部分:
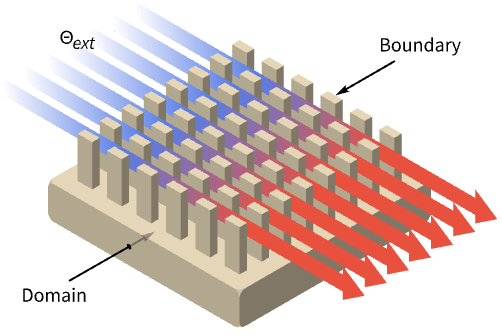
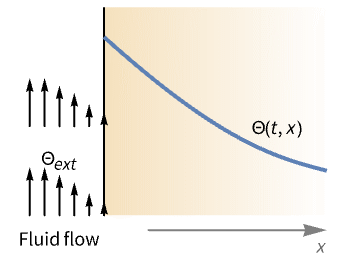
- HeatTransferValue 通常用于模拟仿真区域之外的冷却或加热流的影响. 常见的示例包括散热器.
- HeatTransferValue 对越过边界传递的热能进行建模,其中因变量为温度
 (单位为 [
(单位为 [![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/HeatTransferValue.zh/4.png) ]),自变量为
]),自变量为 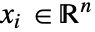 (单位为 [
(单位为 [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/HeatTransferValue.zh/6.png) ]),时间变量为
]),时间变量为 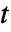 (单位为 [
(单位为 [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/HeatTransferValue.zh/8.png) ]).
]). - 平稳变量 vars 为 vars={Θ[x1,…,xn],{x1,…,xn}}.
- 与时间相关的变量 vars 为 vars={Θ[t,x1,…,xn],t,{x1,…,xn}}.
- 非保守时变传热模型 HeatTransferPDEComponent 基于对流扩散模型,其中质量密度为
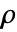 ,比热容为
,比热容为 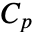 ,导热系数为
,导热系数为 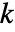 ,对流速度矢量为
,对流速度矢量为 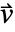 ,热源为
,热源为 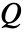 :
: - 传热值 HeatTransferValue (其中传热系数
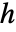 (单位为 [
(单位为 [![TemplateBox[{InterpretationBox[, 1], {"W", , "/(", , {"m", ^, 2}, , "K", , ")"}, watts per meter squared kelvin, {{(, "Watts", )}, /, {(, {{"Meters", ^, 2}, , "Kelvins"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"W", , "/(", , {"m", ^, 2}, , "K", , ")"}, watts per meter squared kelvin, {{(, "Watts", )}, /, {(, {{"Meters", ^, 2}, , "Kelvins"}, )}}}, QuantityTF]](Files/HeatTransferValue.zh/16.png) ]),外部温度
]),外部温度 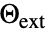 (单位为 [
(单位为 [![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/HeatTransferValue.zh/18.png) ]),边界单位法线
]),边界单位法线 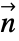 )模拟:
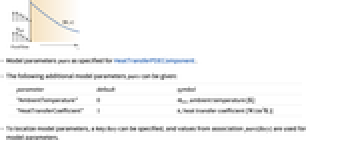
)模拟: - 模型参数 pars 与 HeatTransferPDEComponent 所指定的相同.
- 还可以给出以下模型参数 pars:
-
参数 缺省值 符号 "AmbientTemperature" - 0
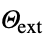 ,环境温度,单位为 [
,环境温度,单位为 [![TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "K", kelvins, "Kelvins"}, QuantityTF]](Files/HeatTransferValue.zh/23.png) ]
]"HeatTransferCoefficient" 
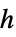 ,传热系数,单位为 [
,传热系数,单位为 [![TemplateBox[{InterpretationBox[, 1], {"W", , "/(", , {"m", ^, 2}, , "K", , ")"}, watts per meter squared kelvin, {{(, "Watts", )}, /, {(, {{"Meters", ^, 2}, , "Kelvins"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"W", , "/(", , {"m", ^, 2}, , "K", , ")"}, watts per meter squared kelvin, {{(, "Watts", )}, /, {(, {{"Meters", ^, 2}, , "Kelvins"}, )}}}, QuantityTF]](Files/HeatTransferValue.zh/26.png) ]
] - 如要本地化模型参数,可以指定键 lkey,并使用来自关联 pars[lkey] 的值作为模型参数.
- 所有模型参数都可能取决于
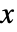 、
、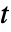 和
和  中的任何一个,以及其他因变量.
中的任何一个,以及其他因变量. - HeatTransferValue 是 HeatFluxValue 的特殊情形.
- HeatTransferValue 运算为广义的 NeumannValue.
- 边界谓词 pred 可以像在 NeumannValue 中一样指定.
- 如果 HeatTransferValue 取决于在关联 pars 中指定为 …,keypi…,pivi,…] 的参数
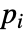 ,则参数
,则参数 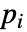 用
用 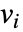 替换.
替换.
范例
打开所有单元关闭所有单元基本范例 (2)
范围 (4)
基本范例 (2)
二维 (1)
Wolfram Research (2020),HeatTransferValue,Wolfram 语言函数,https://reference.wolfram.com/language/ref/HeatTransferValue.html.
文本
Wolfram Research (2020),HeatTransferValue,Wolfram 语言函数,https://reference.wolfram.com/language/ref/HeatTransferValue.html.
CMS
Wolfram 语言. 2020. "HeatTransferValue." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/HeatTransferValue.html.
APA
Wolfram 语言. (2020). HeatTransferValue. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HeatTransferValue.html 年