HermitianMatrix

HermitianMatrix[hmat]

将厄米特矩阵 hmat 转换为结构化数组.

更多信息和选项

  • 当厄米特矩阵表示为结构化数组时，便于进行指定.
  • 对于厄米特矩阵，这样可大幅降低求解应用中出现的特征问题所花费的成本.
  • 厄米特矩阵 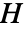满足 H〚i,j〛=TemplateBox[{{H, 〚, {j, ,, i}, 〛}}, Conjugate].
  • 元素 hij 不必是数值.
  • 一般情况下，厄米特矩阵的逆矩阵以及厄米特矩阵的矩阵函数运算结果也是厄米特矩阵.
  • 对于 HermitianMatrix sa，可通过 sa["prop"] 获取以下属性 "prop"：
  • "Matrix"以完整数组表示的厄米特矩阵
    "Properties"支持的属性的列表
    "Structure"结构化数组的类型
    "StructuredData"结构化数组存储的内部数据
    "StructuredAlgorithms"含有针对结构化数组的特殊方法的函数的列表
    "Summary"摘要信息，以 Dataset 的方式表示
  • Normal[HermitianMatrix[…]] 以普通矩阵的形式给出厄米特矩阵.
  • HermitianMatrix[…,TargetStructure->struct] 以 struct 指定的格式返回厄米特矩阵. 可能的设置包括：
  • Automatic自动选择以何种格式表示矩阵
    "Dense"用稠密矩阵表示
    "Structured"用结构化数组表示
  • HermitianMatrix[…,TargetStructureAutomatic] 等价于 HermitianMatrix[…,TargetStructure"Structured"].

范例

打开所有单元关闭所有单元

基本范例  (1)

构建厄米特矩阵：

显示元素：

Normal 可以将 HermitianMatrix 转换为普通表示方式：

范围  (4)

根据上三角项构建厄米特矩阵：

显示元素：

也可以根据下三角项构建厄米特矩阵：

希尔伯特矩阵是厄米特矩阵：

复反射矩阵既是厄米特矩阵，也是酉矩阵：

HermitianMatrix 对象包含提供有关矩阵信息的属性：


"Summary" 属性给出了有关矩阵的信息的简要总结：

"StructuredAlgorithms" 属性列出了具有结构化算法的函数：

选项  (1)

TargetStructure  (1)

以稠密矩阵的形式返回厄米特矩阵：

以结构化数组的形式返回厄米特矩阵：

应用  (3)

根据 GaussianUnitaryMatrixDistribution 构建的矩阵是厄米特矩阵：

根据 GaussianSymplecticMatrixDistribution 构建的矩阵是厄米特矩阵：

Pauli 矩阵是厄米特矩阵：

正定厄米特矩阵 定义了内积 ：

验证 是正定矩阵：

对 TemplateBox[{}, Complexes]^n 的标准基进行正交化以找到标准正交基：

确认该基相对于内积 是正交的：

属性和关系  (4)

厄米特矩阵的共轭转置等于原始矩阵：

实对称矩阵也是厄米特矩阵：

可用 SymmetrizedArray 或 HermitianMatrix 表示厄米特矩阵：

这两种表示形式是相同的，但支持不同的算法：

SymmetrizedArray 支持张量运算，如 D、Flatten、Inner 和 Outer：

HermitianMatrix 支持特定于矩阵的运算，如 KroneckerProduct：

也可用 SymmetricMatrix 表示实厄米特矩阵：

对于复厄米特矩阵则不然：

Wolfram Research (2024)，HermitianMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HermitianMatrix.html.

文本

Wolfram Research (2024)，HermitianMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/HermitianMatrix.html.

CMS

Wolfram 语言. 2024. "HermitianMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/HermitianMatrix.html.

APA

Wolfram 语言. (2024). HermitianMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HermitianMatrix.html 年

BibTeX

@misc{reference.wolfram_2024_hermitianmatrix, author="Wolfram Research", title="{HermitianMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/HermitianMatrix.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_hermitianmatrix, organization={Wolfram Research}, title={HermitianMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/HermitianMatrix.html}, note=[Accessed: 22-November-2024 ]}