SymmetricMatrixQ

SymmetricMatrixQ[m]

gives True if m is explicitly symmetric, and False otherwise.

Details and Options

  • A matrix m is symmetric if m==Transpose[m].
  • SymmetricMatrixQ works for symbolic as well as numerical matrices.
  • The following options can be given:
  • SameTest Automaticfunction to test equality of expressions
    Tolerance Automatictolerance for approximate numbers
  • For exact and symbolic matrices, the option SameTest->f indicates that two entries mij and mkl are taken to be equal if f[mij,mkl] gives True.
  • For approximate matrices, the option Tolerance->t can be used to indicate that all entries Abs[mij]≤t are taken to be zero.
  • For matrix entries Abs[mij]>t, equality comparison is done except for the last 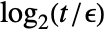bits, where 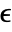is $MachineEpsilon for MachinePrecision matrices and 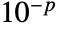for matrices of Precision .

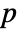Examples

open allclose all

Basic Examples  (2)

Test if a 2×2 numeric matrix is explicitly symmetric:

Test if a 3×3 symbolic matrix is explicitly symmetric:

Scope  (10)

Basic Uses  (6)

Test if a real machine-precision matrix is symmetric:

A real symmetric matrix is also Hermitian:

Test if a complex matrix is symmetric:

A complex symmetric matrix has symmetric real and imaginary parts:

Test if an exact matrix is symmetric:

Make the matrix symmetric:

Use SymmetricMatrixQ with an arbitrary-precision matrix:

A random matrix is typically not symmetric:

Use SymmetricMatrixQ with a symbolic matrix:

The matrix becomes symmetric when :

SymmetricMatrixQ works efficiently with large numerical matrices:

Special Matrices  (4)

Use SymmetricMatrixQ with sparse matrices:

Use SymmetricMatrixQ with structured matrices:

Use with a QuantityArray structured matrix:

The identity matrix is symmetric:

HilbertMatrix is symmetric:

Options  (2)

SameTest  (1)

This matrix is symmetric for a positive real , but SymmetricMatrixQ gives False:

Use the option SameTest to get the correct answer:

Tolerance  (1)

Generate a real-valued symmetric matrix with some random perturbation of order 10-14:

Adjust the option Tolerance to accept this matrix as symmetric:

The norm of the difference between the matrix and its transpose:

Applications  (13)

Generating Symmetric Matrices  (4)

Any matrix generated from a symmetric function is symmetric:

The function is symmetric:

Using Table generates a symmetric matrix:

SymmetrizedArray can generate matrices (and general arrays) with symmetries:

Convert back to an ordinary matrix using Normal:

Check that matrices drawn from GaussianOrthogonalMatrixDistribution are symmetric:

Matrices drawn from CircularOrthogonalMatrixDistribution are symmetric and unitary:

Every Jordan matrix is similar to a symmetric matrix. Since any square matrix is similar to its Jordan form, this means that any square matrix is similar to a symmetric matrix. Define a function for generating an Jordan block for eigenvalue :

For example, here is the Jordan matrix of dimension 4 for the eigenvalue :

Define a function for generating a corresponding complex similarity transformation:

The matrix is a sum of times the identity matrix and times the backward identity matrix:

Then s(n).j(lambda,n).TemplateBox[{{s, (, n, )}}, Inverse] is symmetric, which shows that the Jordan matrix is similar to a symmetric matrix:

Confirm the matrix is symmetric:

Examples of Symmetric Matrices  (5)

The Hessian matrix of a function is symmetric:

Many special matrices are symmetric, including FourierMatrix:

HadamardMatrix:

HankelMatrix:

And HilbertMatrix:

Visualize the matrix types:

Many filter kernel matrices are symmetric, including DiskMatrix:

CrossMatrix:

DiamondMatrix:

Visualize the matrices:

AdjacencyMatrix of an undirected graph is symmetric:

As is KirchhoffMatrix:

Visualize adjacency and Kirchhoff matrices for different graphs:

Several statistical measures are symmetric matrices, including Covariance:

Correlation:

AbsoluteCorrelation:

Uses of Symmetric Matrices  (4)

A positive-definite, real symmetric matrix or metric defines an inner product by :

Verify that is in fact symmetric and positive definite:

Orthogonalize the standard basis of TemplateBox[{}, Reals]^n to find an orthonormal basis:

Confirm that this basis is orthonormal with respect to the inner product :

The moment of inertia tensor is the equivalent of mass for rotational motion. For example, kinetic energy is , with taking the place of the mass and angular velocity taking the place of linear velocity in the formula . can be represented by a positive-definite symmetric matrix. Compute the moment of inertia for a tetrahedron with endpoints at the origin and positive coordinate axes:

Verify that the matrix is symmetric:

Compute the kinetic energy if its angular velocity is :

The kinetic energy is positive as long as is nonzero, showing the matrix was positive definite:

Determine if a sparse matrix is structurally symmetric:

The matrix is not symmetric:

But it is structurally symmetric:

Use a different method for symmetric matrices, with failover to a general method:

Construct real-valued matrices for testing:

For a non-symmetric matrix m, the function myLS just uses Gaussian elimination:

For a symmetric indefinite matrix ms, try Cholesky and continue with Gaussian elimination:

For a symmetric positive-definite matrix mpd, try Cholesky, which succeeds:

Properties & Relations  (14)

SymmetricMatrixQ[x] trivially returns False for any x that is not a matrix:

A matrix is symmetric if mTranspose[m]:

A real-valued symmetric matrix is Hermitian:

But a complex-valued symmetric matrix may not be:

Use Symmetrize to compute the symmetric part of a matrix:

This equals the average of m and Transpose[m]:

Any matrix can be represented as the sum of its symmetric and antisymmetric parts:

Use AntisymmetricMatrixQ to test whether a matrix is antisymmetric:

If is a symmetric matrix with real entries, then is antihermitian:

MatrixExp[I m] for real symmetric m is unitary:

A real-valued symmetric matrix is always a normal matrix:

A complex-valued symmetric matrix need not be normal:

Real-valued symmetric matrices have all real eigenvalues:

Use Eigenvalues to find eigenvalues:

Note that a complex-valued symmetric matrix may have both real and complex eigenvalues:

CharacteristicPolynomial[m,x] for real symmetric m can be factored into linear terms:

Real-valued symmetric matrices have a complete set of eigenvectors:

As a consequence, they must be diagonalizable:

Use Eigenvectors to find eigenvectors:

Note that a complex-valued symmetric matrix need not have these properties:

The inverse of a symmetric matrix is symmetric:

Matrix functions of symmetric matrices are symmetric, including MatrixPower:

MatrixExp:

And any univariate function representable using MatrixFunction:

SymmetricMatrix can be used to explicitly construct symmetric matrices:

These satisfy SymmetricMatrixQ:

Possible Issues  (1)

SymmetricMatrixQ uses the definition TemplateBox[{m}, Transpose]=m for both real- and complex-valued matrices:

These complex matrices need not be normal or possess many properties of self-adjoint (real symmetric) matrices:

HermitianMatrixQ tests the condition TemplateBox[{m}, ConjugateTranspose]=m for self-adjoint matrices:

Alternatively, test if the entries are real to restrict to real symmetric matrices:

Neat Examples  (1)

Images of symmetric matrices including FourierMatrix:

Wolfram Research (2008), SymmetricMatrixQ, Wolfram Language function, https://reference.wolfram.com/language/ref/SymmetricMatrixQ.html (updated 2014).

Text

Wolfram Research (2008), SymmetricMatrixQ, Wolfram Language function, https://reference.wolfram.com/language/ref/SymmetricMatrixQ.html (updated 2014).

CMS

Wolfram Language. 2008. "SymmetricMatrixQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/SymmetricMatrixQ.html.

APA

Wolfram Language. (2008). SymmetricMatrixQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SymmetricMatrixQ.html

BibTeX

@misc{reference.wolfram_2025_symmetricmatrixq, author="Wolfram Research", title="{SymmetricMatrixQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/SymmetricMatrixQ.html}", note=[Accessed: 09-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_symmetricmatrixq, organization={Wolfram Research}, title={SymmetricMatrixQ}, year={2014}, url={https://reference.wolfram.com/language/ref/SymmetricMatrixQ.html}, note=[Accessed: 09-July-2025 ]}