I

I     表示虚数单位 .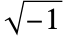

更多信息

范例

打开所有单元关闭所有单元

基本范例  (3)

I 的格式为 :

的排版形式可以输入为 ii（表示“虚数 i”）：

从负实数的平方根生成：

在精确和近似的计算中用 I：

范围  (2)

内置的数学函数适用于复数：

提取虚部：

推广和延伸  (6)

用 jj 输入 I 的工程符号 ：

作为无穷量的一个方向：

作为 Limit 的一个方向：

作为扩张域的生成元：

在高斯整数环内做因子分解：

作为级数的展开点：

应用  (2)

把一个复数从极坐标形式转换为矩形形式：

圆柱绕流可以作为一个复数值函数的实部：

属性和关系  (12)

I 被表示一个没有实部的复数：

I 是一个精确数：

用 ComplexExpand 提取实部和虚部：

用 ExpToTrig 将包含 I 的指数转换为三角形式：

化简包含 I 的表达式：

I 是一个代数数：

纯虚数参数的三角函数被求值为简单形式：

在多项式方程的解中获取 I：

二次多项式的根可以被求值为复数：

用 Chop 清除较小虚部：

用 I 作为积分极限：

按虚部递增来对数进行排序：

可能存在的问题  (6)

求值复数是原子对象，不明确包含 I：

形式为 Complex[x_,y_] 的模式可用于匹配整个复数：

如果 I 位于一个“保持”的表达式中，它就不会成为一个带有头部 Complex 的表达式：

与运算格式进行比较：

特别是，未运算的 I 是一个符号，而不是一个数字：

I 的机器精度计算产生一个近似 0 值的实部：

任意精度计算产生一个精确 0 值的实部：

包含 I 的仿纯实数量不能用于数值比较中：

使用 FullSimplify 或 ComplexExpand 先转换为明显为实数的表达式：

有限的虚数量会被无穷的实数量或复数量吸收：

I 不能用在区间中：

巧妙范例  (2)

I 的嵌套幂：

求以解析式表示的极限：

生成 I 的幂的所有可能的嵌套形式：

在复平面上绘制点：

Wolfram Research (1988)，I，Wolfram 语言函数，https://reference.wolfram.com/language/ref/I.html （更新于 2002 年）.

文本

Wolfram Research (1988)，I，Wolfram 语言函数，https://reference.wolfram.com/language/ref/I.html （更新于 2002 年）.

CMS

Wolfram 语言. 1988. "I." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2002. https://reference.wolfram.com/language/ref/I.html.

APA

Wolfram 语言. (1988). I. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/I.html 年

BibTeX

@misc{reference.wolfram_2024_i, author="Wolfram Research", title="{I}", year="2002", howpublished="\url{https://reference.wolfram.com/language/ref/I.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_i, organization={Wolfram Research}, title={I}, year={2002}, url={https://reference.wolfram.com/language/ref/I.html}, note=[Accessed: 22-November-2024 ]}