Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

InfiniteLineThrough

InfiniteLineThrough[{p₁,p₂,…}]

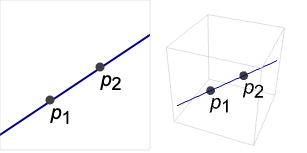
给出穿过点 p_i 的无限长直线.

更多信息

InfiniteLineThrough 通常用来指定 GeometricScene 中的点约束条件.
可能的情况下，InfiniteLineThrough 给出明确的 InfiniteLine 对象.
InfiniteLineThrough[{p₁,p₂,…}] 中的 p_i 可以是一组坐标或明确的 Point 对象.

InfiniteLineThrough 可与 GeometricScene 中的符号点和量一起使用，规定它们必须在一条直线上.

范例

打开所有单元关闭所有单元

基本范例 (2)

穿过三个点的无限长直线：

显示该直线：

从无限长直线到一个点的 RegionDistance：

范围 (2)

InfiniteLineThrough 适用于坐标：

多个点：

一组点：

InfiniteLineThrough 适用于一维空间中的点：

2D：

D：

应用 (3)

基本应用 (3)

可视化穿过三个点的直线：

求通过三个点的圆的隐式表示：

参数化表示：

求拟合一组点的最佳 InfiniteLine：

用 RegionFit 求最佳拟合：

比较结果：

属性和关系 (2)

InfiniteLineThrough 返回一个 InfiniteLine 对象：

用 RegionFit 获取拟合一组点的最佳 InfiniteLine：

顶部