InverseRadonTransform[expr,{p,ϕ},{x,y}]
gives the inverse Radon transform of expr.


InverseRadonTransform
InverseRadonTransform[expr,{p,ϕ},{x,y}]
gives the inverse Radon transform of expr.
Details and Options

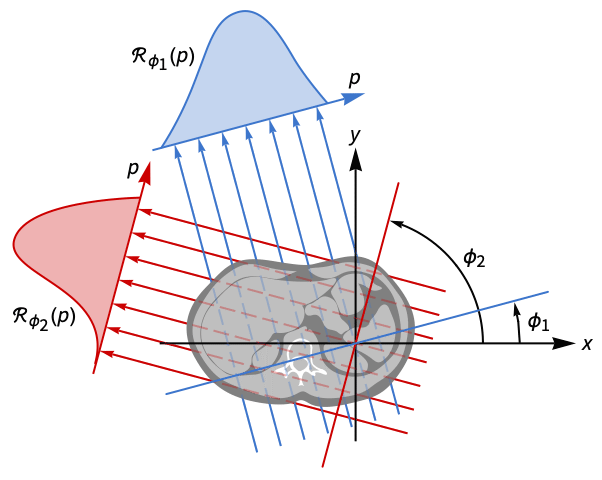
- The inverse Radon transform provides the mathematical basis for tomographic image reconstruction.
- Geometrically, the inversion procedure recovers an image from the values of its Radon transform along different projections of the image for fixed angles
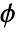 and varying
and varying 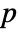 .
. - InverseRadonTransform computes a radial Fourier transform, followed by a two-dimensional inverse Fourier transform, to accomplish the above inversion. »
- The following options can be given:
-
Assumptions $Assumptions assumptions on parameters GenerateConditions False whether to generate results that involve conditions on parameters Method Automatic what method to use - In TraditionalForm, InverseRadonTransform is output using
![TemplateBox[{{f, (, {p, ,, phi}, )}, p, phi, x, y}, InverseRadonTransform] TemplateBox[{{f, (, {p, ,, phi}, )}, p, phi, x, y}, InverseRadonTransform]](Files/InverseRadonTransform.en/4.png) .
.
Examples
open all close allBasic Examples (1)
Scope (5)
Basic Uses (1)
Gaussian Functions (2)
Piecewise and Generalized Functions (2)
Inverse Radon transform of a piecewise function:
Inverse Radon transform of an expression involving DiracDelta:
Applications (2)
Compute the symbolic inverse Radon transform of a function:
Obtain the same result using InverseRadon:
Use the Radon transform to solve a Poisson equation:
Apply RadonTransform to the equation:
Solve the ordinary differential equation using DSolveValue:
Set the arbitrary constants in the solution to 0:
Obtain the solution for the original equation using InverseRadonTransform:
Properties & Relations (3)
InverseRadonTransform and RadonTransform are mutual inverses:
InverseRadonTransform is a linear operator:
Compute the inverse Radon transform using Fourier transforms:
Find the Fourier transform with respect to p:
Express the result in terms of a unit vector ξ = { u1,u2}, assuming that ![]() :
:
Compute the inverse Fourier transform with respect to { u1,u2}:
Obtain the same result directly using InverseRadonTransform:
Related Guides
History
Text
Wolfram Research (2017), InverseRadonTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseRadonTransform.html.
CMS
Wolfram Language. 2017. "InverseRadonTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseRadonTransform.html.
APA
Wolfram Language. (2017). InverseRadonTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseRadonTransform.html
BibTeX
@misc{reference.wolfram_2025_inverseradontransform, author="Wolfram Research", title="{InverseRadonTransform}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/InverseRadonTransform.html}", note=[Accessed: 27-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_inverseradontransform, organization={Wolfram Research}, title={InverseRadonTransform}, year={2017}, url={https://reference.wolfram.com/language/ref/InverseRadonTransform.html}, note=[Accessed: 27-February-2026]}