InverseRadonTransform

InverseRadonTransform[expr,{p,ϕ},{x,y}]

gives the inverse Radon transform of expr.

Details and Options

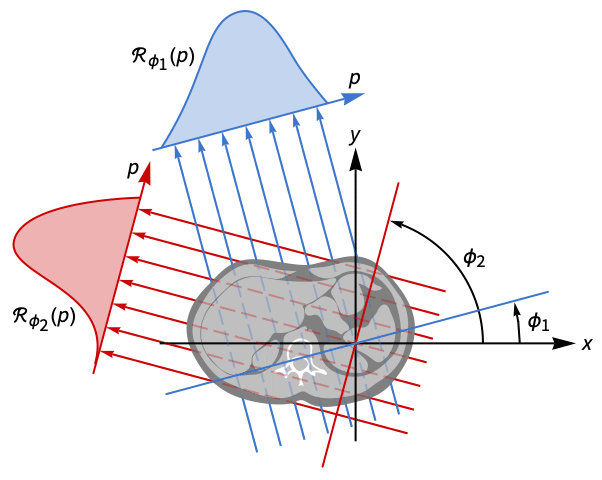
  • The inverse Radon transform provides the mathematical basis for tomographic image reconstruction.
  • Geometrically, the inversion procedure recovers an image from the values of its Radon transform along different projections of the image for fixed angles 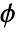and varying .
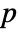  • InverseRadonTransform computes a radial Fourier transform, followed by a two-dimensional inverse Fourier transform, to accomplish the above inversion. »
  • The following options can be given:
  • Assumptions$Assumptionsassumptions on parameters
    GenerateConditionsFalsewhether to generate results that involve conditions on parameters
    MethodAutomaticwhat method to use
  • In TraditionalForm, InverseRadonTransform is output using TemplateBox[{{f, (, {p, ,, phi}, )}, p, phi, x, y}, InverseRadonTransform].

Examples

open allclose all

Basic Examples  (1)

Compute the inverse Radon transform of a function:

Plot the function along with the inverse transform:

Scope  (5)

Basic Uses  (1)

Compute the inverse Radon transform of a function for symbolic parameter values:

Use exact values for the parameters:

Use inexact values for the parameters:

Gaussian Functions  (2)

Inverse Radon transform of a Gaussian function:

Plot the function along with the inverse transform:

Polynomial Gaussian function:

Product of a polynomial Gaussian function with trigonometric functions:

Piecewise and Generalized Functions  (2)

Inverse Radon transform of a piecewise function:

Inverse Radon transform of an expression involving DiracDelta:

Applications  (2)

Compute the symbolic inverse Radon transform of a function:

Obtain the same result using InverseRadon:

Use the Radon transform to solve a Poisson equation:

Apply RadonTransform to the equation:

Solve the ordinary differential equation using DSolveValue:

Set the arbitrary constants in the solution to 0:

Obtain the solution for the original equation using InverseRadonTransform:

Verify the solution:

Plot the solution:

Properties & Relations  (3)

InverseRadonTransform and RadonTransform are mutual inverses:

InverseRadonTransform is a linear operator:

Compute the inverse Radon transform using Fourier transforms:

Find the Fourier transform with respect to p:

Express the result in terms of a unit vector ξ = { u1,u2}, assuming that k=TemplateBox[{xi}, Abs]:

Compute the inverse Fourier transform with respect to { u1,u2}:

Obtain the same result directly using InverseRadonTransform:

Neat Examples  (1)

Create a table of inverse Radon transforms:

Wolfram Research (2017), InverseRadonTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseRadonTransform.html.

Text

Wolfram Research (2017), InverseRadonTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseRadonTransform.html.

CMS

Wolfram Language. 2017. "InverseRadonTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseRadonTransform.html.

APA

Wolfram Language. (2017). InverseRadonTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseRadonTransform.html

BibTeX

@misc{reference.wolfram_2024_inverseradontransform, author="Wolfram Research", title="{InverseRadonTransform}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/InverseRadonTransform.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_inverseradontransform, organization={Wolfram Research}, title={InverseRadonTransform}, year={2017}, url={https://reference.wolfram.com/language/ref/InverseRadonTransform.html}, note=[Accessed: 18-November-2024 ]}