takes the series s, and gives a series for the inverse of the function represented by s.
InverseSeries[s,x]
uses the variable x in the inverse series.


InverseSeries
takes the series s, and gives a series for the inverse of the function represented by s.
InverseSeries[s,x]
uses the variable x in the inverse series.
Details
- InverseSeries performs "reversion" of series.
- Given a series
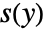 , InverseSeries[s,x] gives a series for
, InverseSeries[s,x] gives a series for 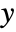 such that
such that 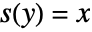 .
. - InverseSeries can be applied to any SeriesData object with the appropriate structure, whether or not it has been generated by Series.
Examples
open all close allBasic Examples (3)
Applications (2)
See Also
Related Guides
History
Introduced in 1988 (1.0)
Text
Wolfram Research (1988), InverseSeries, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseSeries.html.
CMS
Wolfram Language. 1988. "InverseSeries." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseSeries.html.
APA
Wolfram Language. (1988). InverseSeries. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseSeries.html
BibTeX
@misc{reference.wolfram_2025_inverseseries, author="Wolfram Research", title="{InverseSeries}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/InverseSeries.html}", note=[Accessed: 15-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_inverseseries, organization={Wolfram Research}, title={InverseSeries}, year={1988}, url={https://reference.wolfram.com/language/ref/InverseSeries.html}, note=[Accessed: 15-January-2026]}