WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

InverseSeries[s]

級数 s を取り，s で表される関数の逆関数について級数を与える．

InverseSeries[s,x]

逆の級数で変数 x を使う．

詳細
Details and Options Details and Options
例題  
例  
一般化と拡張  
アプリケーション  
特性と関係  
関連項目
テクニカルノート
関連するガイド
履歴
引用書式

InverseSeries

InverseSeries[s]

級数 s を取り，s で表される関数の逆関数について級数を与える．

InverseSeries[s,x]

逆の級数で変数 x を使う．

詳細

  • InverseSeriesは，級数の「逆行」を実行する．
  • 級数 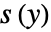について，InverseSeries[s,x]は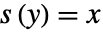，となる 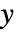の級数を与える．
  • Seriesによって作成されているいないにかかわらず，InverseSeriesは適当な構造を持っているSeriesDataオブジェクトに適用される．

例題

すべて開く すべて閉じる

例  (3)

x Sin[x]の逆関数の級数を求める：

Wolfram Language code: InverseSeries[Series[x Sin[x], {x, 0, 10}]]

Sin[x]の逆関数の級数を求める：

Wolfram Language code: InverseSeries[Series[Sin[x], {x, 0, 10}]]
Wolfram Language code: Series[ArcSin[x], {x, 0, 10}]

明示的に指定された級数で表される関数の逆関数の級数を求める：

Wolfram Language code: InverseSeries[x ^ 2 + 3x ^ 4 + O[x] ^ 8]

もとの関数に戻るために再び逆にする：

Wolfram Language code: InverseSeries[%]

一般化と拡張  (1)

級数を逆にする．結果は変数yについて与える：

Wolfram Language code: InverseSeries[1 + 2 x + 3x ^ 2 + O[x] ^ 5, y]

アプリケーション  (2)

付近の f[x]の根について，ニュートン(Newton)近似でより高い次数の項を求める：

Wolfram Language code: InverseSeries[Series[f[x], {x, a, 3}]]
Wolfram Language code: Normal[%] /. x -> 0

であるとして，原点におけるの級数展開を計算する：

Wolfram Language code: serf = x + c1 x ^ 2 + c2 x ^ 3 + c3 x ^ 4 + c4 x ^ 5 + O[x] ^ 6; serg = x + d1 x ^ 2 + d2 x ^ 3 + d3 x ^ 4 + d4 x ^ 5 + O[x] ^ 6;
Wolfram Language code: serCommute[s1_, s2_] := ComposeSeries[s1, s2] - ComposeSeries[s2, s1]
Wolfram Language code: serCommute[serf, serg] / serCommute[InverseSeries[serf], InverseSeries[serg]]//Simplify

特性と関係  (1)

もとの級数を用いて逆級数を構築すると恒等関数が返される：

Wolfram Language code: s = 1 + 2 x + 3x ^ 2 + O[x] ^ 5;
Wolfram Language code: ComposeSeries[InverseSeries[s], s]
Wolfram Research (1988), InverseSeries, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseSeries.html.

テキスト

Wolfram Research (1988), InverseSeries, Wolfram言語関数， https://reference.wolfram.com/language/ref/InverseSeries.html.

CMS

Wolfram Language. 1988. "InverseSeries." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseSeries.html.

APA

Wolfram Language. (1988). InverseSeries. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseSeries.html

BibTeX

@misc{reference.wolfram_2026_inverseseries, author="Wolfram Research", title="{InverseSeries}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/InverseSeries.html}", note=[Accessed: 19-July-2026]}

BibLaTeX

@online{reference.wolfram_2026_inverseseries, organization={Wolfram Research}, title={InverseSeries}, year={1988}, url={https://reference.wolfram.com/language/ref/InverseSeries.html}, note=[Accessed: 19-July-2026]}