KroneckerSymbol
KroneckerSymbol[n,m]
给出克罗内克符号 ![]() .
.
更多信息

- KroneckerSymbol 亦称为雅可比符号或勒让德符号.
- 整型数学函数,同时适合符号和数值运算.
- KroneckerSymbol[n,1] 给出 1.
- 当 n 非负时,KroneckerSymbol[n,-1] 给出 1,其他情况给出
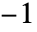 .
. - 对于数字
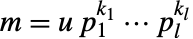 ,其中
,其中 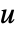 为单位值,
为单位值,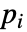 为质数,
为质数,![TemplateBox[{n, m}, KroneckerSymbol] TemplateBox[{n, m}, KroneckerSymbol]](Files/KroneckerSymbol.zh/6.png) 返回
返回 ![TemplateBox[{n, u}, KroneckerSymbol] TemplateBox[{n, {p, _, 1}}, KroneckerSymbol] ...TemplateBox[{n, {p, _, l}}, KroneckerSymbol] TemplateBox[{n, u}, KroneckerSymbol] TemplateBox[{n, {p, _, 1}}, KroneckerSymbol] ...TemplateBox[{n, {p, _, l}}, KroneckerSymbol]](Files/KroneckerSymbol.zh/7.png) .
.
范例
打开所有单元关闭所有单元基本范例 (2)
范围 (9)
数值运算 (3)
符号运算 (6)
应用 (11)
数论 (9)
对于模 p 的同余整数 m 和 n,KroneckerSymbol[m,p]==KroneckerSymbol[n,p]:
求基为 ![]() 的 Euler–Jacobi 伪素数: [更多信息]
的 Euler–Jacobi 伪素数: [更多信息]
如果 KroneckerSymbol[a,p] == 1,则同余方程 ![]() 有解:
有解:
对于奇整数 k,KroneckerSymbol[n,k] 是模 k 的实 DirichletCharacter:
可用 KroneckerSymbol[χ[-1]k,n] 来表示模 k 的实主特征 χ:
可用与 k 互质的整数的 KroneckerSymbol 表示实数非主特征:
KroneckerSymbol 是雅可比符号对所有整数的推广:
属性和关系 (5)
对于非互质整数,KroneckerSymbol 给出 ![]() :
:
对于每个参数,KroneckerSymbol 都是完全积性函数:
用 KroneckerSymbol 计算模 k 的实 DirichletCharacter,k 为奇整数:
巧妙范例 (4)
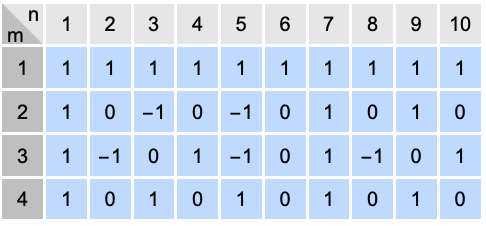
KroneckerSymbol 的阵列图:
绘制 KroneckerSymbol 的傅立叶变换的参数:
模 2 的 KroneckerSymbol 的递差:
绘制 KroneckerSymbol 的 Ulam 螺旋:
文本
Wolfram Research (2007),KroneckerSymbol,Wolfram 语言函数,https://reference.wolfram.com/language/ref/KroneckerSymbol.html.
CMS
Wolfram 语言. 2007. "KroneckerSymbol." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/KroneckerSymbol.html.
APA
Wolfram 语言. (2007). KroneckerSymbol. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/KroneckerSymbol.html 年