WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

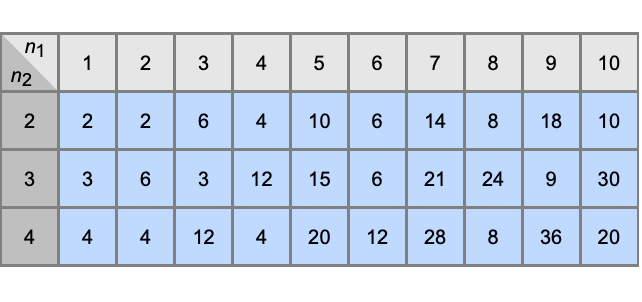
LCM[n1,n2,…]

niの最小公倍数(LCM)を返す．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
数値評価  
記号演算  
アプリケーション  
基本的なアプリケーション  
整数論  
特性と関係  
考えられる問題  
インタラクティブな例題  
おもしろい例題  
関連項目
テクニカルノート
関連するガイド
関連リンク
履歴
引用書式

LCM

LCM[n1,n2,…]

niの最小公倍数(LCM)を返す．

詳細

  • LCMは最小公倍数として知られている．
  • 記号操作・数値操作の両方に適した数学的整数関数である．
  • LCM[n1,n2,…]は整数 n1,n2,…のそれぞれの倍数である最小の正の整数である．
  • 有理数 riについて，LCM[r1,r2,…]はすべての r/riが整数となる最大の有理数 r を返す．
  • LCMはガウス整数上で作用する．

例題

すべて開く すべて閉じる

例  (2)

数の集合の最小公倍数を求める：

と別の数の最小公倍数をプロットする：

スコープ  (11)

数値評価  (7)

LCMは整数に使うことができる：

ガウス整数：

実有理数：

複素有理数：

1引数の形は正の整数については恒等式である：

大きい整数について計算する：

LCMは要素単位でリストに縫い込まれる：

記号演算  (4)

TraditionalFormによる表示：

不等式を簡約する：

方程式を解く：

式を簡約する：

アプリケーション  (9)

基本的なアプリケーション  (4)

整数の最初の100組のペアの最小公倍数の表：

2つの整数の最小公倍数を可視化する：

フィボナッチ(Fibonacci)数：

最初の100個の整数のLCM：

正の整数についてLCMを計算する：

以下と比較する：

整数論  (5)

累積的最小公倍数：

データの対数をプロットする（リーマン(Riemann)仮説が成立するなら，これは線形に増加する）：

最初の n 個の整数のMangoldtLambdaの和は，最初の n 個の整数のLCMの自然対数に等しい：

位数 n の対称群からの群の元の最大位数（ランダウ(Landau)の関数）：

二項係数の最小公倍数：

以下と比較する：

LCMを含む式を簡約する：

特性と関係  (7)

a と b の約数はすべて の約数である：

GCDを使ってLCMを計算する：

以下と比較する：

互いに素な数のLCMはその積に等しい：

素数のLCMはその積である：

素数ベキ表現のLCM ：

LCMは可換である ：

LCMは結合律を満たす ：

LCMは分配律を満たす ：

LCMを使ってMangoldtLambdaを計算する：

以下と比較する：

考えられる問題  (3)

符号は除去される：

引数は明示的な整数でなければならない：

LCMは引数をソートする：

インタラクティブな例題  (1)

3つの数の最小公倍数を可視化する：

おもしろい例題  (4)

フィボナッチ(Fibonacci)数の最小公倍数を可視化する：

LCMのフーリエ変換の引数をプロットする：

LCMのウラム(Ulam)螺線をプロットする：

と有理数の最小公倍数から構築する：

Wolfram Research (1988), LCM, Wolfram言語関数， https://reference.wolfram.com/language/ref/LCM.html （1999年に更新）.

テキスト

Wolfram Research (1988), LCM, Wolfram言語関数， https://reference.wolfram.com/language/ref/LCM.html （1999年に更新）.

CMS

Wolfram Language. 1988. "LCM." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 1999. https://reference.wolfram.com/language/ref/LCM.html.

APA

Wolfram Language. (1988). LCM. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LCM.html

BibTeX

@misc{reference.wolfram_2025_lcm, author="Wolfram Research", title="{LCM}", year="1999", howpublished="\url{https://reference.wolfram.com/language/ref/LCM.html}", note=[Accessed: 18-September-2025]}

BibLaTeX

@online{reference.wolfram_2025_lcm, organization={Wolfram Research}, title={LCM}, year={1999}, url={https://reference.wolfram.com/language/ref/LCM.html}, note=[Accessed: 18-September-2025]}