LaplacianPDETerm[vars]
ラプラス(Laplace)項 ![]() をモデル変数 vars で表す.
をモデル変数 vars で表す.
LaplacianPDETerm[vars,pars]
モデルパラメータ pars を使う.


LaplacianPDETerm
LaplacianPDETerm[vars]
ラプラス(Laplace)項 ![]() をモデル変数 vars で表す.
をモデル変数 vars で表す.
LaplacianPDETerm[vars,pars]
モデルパラメータ pars を使う.
詳細

- ラプラス項は,ポテンシャル,熱移動,音響,構造力学,流体動力学等の多くの物理現象の説明に使われる微分演算子項である.
- LaplacianPDETermは,偏微分方程式の一部として使われる微分演算子項を返す.
- LaplacianPDETermを使って,従属変数
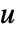 ,独立変数
,独立変数 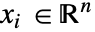 ,時間変数
,時間変数 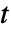 でラプラス方程式がモデル化できる.
でラプラス方程式がモデル化できる. - 定常モデル変数 vars は vars={u[x1,…,xn],{x1,…,xn}}である.
- 従属モデル変数 vars は vars={u[t,x1,…,xn],{x1,…,xn}}または vars={u[t,x1,…,xn],t,{x1,…,xn}}である.
- 拡散係数として
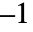 を持つラプラス項
を持つラプラス項 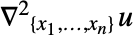 はDiffusionPDETermの
はDiffusionPDETermの 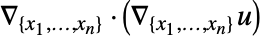 として実現される.
として実現される. - 次は,使用可能なパラメータ pars である.
-
パラメータ デフォルト シンボル "RegionSymmetry" None 
- パラメータ"RegionSymmetry"の可能な選択肢には"Axisymmetric"がある.
- "Axisymmetric"領域対称性は,以下のように角変数を削除することで円筒座標系が削減された切頭円筒座標系を表す.
-
次元 削減 方程式 1D 
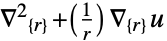
2D 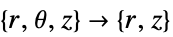
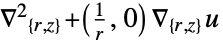
- 拡散係数
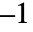 はNeumannValueの意味に影響を与える.
はNeumannValueの意味に影響を与える.
例題
すべて開く すべて閉じるスコープ (3)
項をActivate(アクティブに)する:
アプリケーション (1)
半径5の有限円柱内の ![]() についてのラプラス方程式を解く.解析領域は中空ではない3Dの円柱であるが,この領域が
についてのラプラス方程式を解く.解析領域は中空ではない3Dの円柱であるが,この領域が ![]() 軸について回転対称であるので,軸対称定常LaplacianPDETermが使え,この領域は2D
軸について回転対称であるので,軸対称定常LaplacianPDETermが使え,この領域は2D![]() の切頭円筒座標系で定義できる.
の切頭円筒座標系で定義できる.
計算にかかった合計時間と評価中に使ったメモリ(MB)を出力する:
2D軸対称偏微分モデルを解くための時間とメモリの計算費用は完全な3Dモデルを解くのにかかるそれよりはるかに少ない.完全な3Dモデルを構築する:
記号領域の最適近似と重要部分の細分化のための境界位置を調整しながら完全な3Dモデルを解く:
おもしろい例題 (1)
ラプラス方程式を解くことで迷路から出る道を求める.まず迷路を設定する:
入口を値1のDirichletCondition,出口を値0のDirichletConditionとしてラプラス方程式を解く. DirichletConditionの位置を設定するために領域の境界を求める:
関連するガイド
-
▪
- 偏微分方程式項
テキスト
Wolfram Research (2020), LaplacianPDETerm, Wolfram言語関数, https://reference.wolfram.com/language/ref/LaplacianPDETerm.html (2022年に更新).
CMS
Wolfram Language. 2020. "LaplacianPDETerm." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/LaplacianPDETerm.html.
APA
Wolfram Language. (2020). LaplacianPDETerm. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LaplacianPDETerm.html
BibTeX
@misc{reference.wolfram_2025_laplacianpdeterm, author="Wolfram Research", title="{LaplacianPDETerm}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/LaplacianPDETerm.html}", note=[Accessed: 18-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_laplacianpdeterm, organization={Wolfram Research}, title={LaplacianPDETerm}, year={2022}, url={https://reference.wolfram.com/language/ref/LaplacianPDETerm.html}, note=[Accessed: 18-February-2026]}