LatticeData

LatticeData[lattice,"property"]

格子の指定された特性を返す．

LatticeData[n]

n 次元の名前付きの格子のリストを返す．

詳細

  • 格子は，"FaceCenteredCubic"や"CoxeterTodd"等の一般的な名前で指定することができる．
  • LatticeData[]は，古典的な名前付き格子のリストを返す．
  • LatticeData[patt]は，文字列パターン patt にマッチするすべての名前付き格子のリストを返す．
  • LatticeData[{"type",id},…]は，識別子 id を持つ指定されたタイプの格子のデータを返す．
  • タイプ関連格子
  • {"BarnesWall",n} Barnes–Wall格子 BWn
    {"Bravais",{"system","centering"}}指定の結晶系のためのBravais格子
    {"CoxeterBarnes", {r, n}}Coxeter–Barnes格子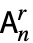
    {"DualRootLattice",group}指定したリー(Lie)群のための二重ルート格子
    {"IntegerLattice",n}整数格子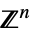
    {"KappaLattice",{m,n}} 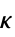格子
    {"LaminatedLattice",{m,n}}層状格子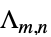
    {"MordellWeil",n}Mordell–Weil格子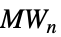
    {"Niemeier",n} 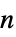次のNiemeier格子
    {"PerfectLattice",n}完全格子
    {"Quebbemann",n}Quebbemann格子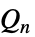
    {"RootLattice",group}指定したリー群のためのルート格子
  • 結晶系は，"Trigonal"，"Monoclinic"等の一般的な名前で指定できる．センタリングは，"FaceCentered"，"BodyCentered"，または"BaseCentered"である．
  • 群は，例えば"A5"あるいは{"A",5}の形で指定できる．
  • LatticeData[group,…]はLatticeData[{"RootLattice",group},…]と等価である．
  • LatticeData["Properties"]は，格子の可能な特性のリストを返す．
  • 格子点特性
  • "Basis"基底ベクトル
    "Determinant"Gram行列の行列式
    "Dimension"格子の次数
    "Dual"二重格子
    "GeneratorMatrix"ジェネレータの行列
    "Genus"格子の種数
    "GlueVectors"粘着ベクトル（適応可能な場合）
    "GramMatrix"Gram行列
    "Image"点の構成（適応可能な場合）
    "KissingNumber"接吻数
    "MinimalNorm"最低基準
    "MinimalVectors"最小ベクトル
    "ModularNumber"モジュール番号
    "RadialFunction"半径の関数としての格子点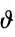（ 級数係数）
    "ThetaSeriesFunction"シータ級数の純関数
  • 格子充填関連特性
  • "CenterDensity"中央密度
    "CoveringRadius"被覆半径
    "CoxeterNumber"コクセター(Coxeter)数
    "Density"平均球面充填密度
    "HermiteInvariant"エルミート(Hermite)不変数
    "PackingRadius"充填半径
    "Thickness"厚さ
    "Volume"基本領域の体積
  • その他の特性
  • "QuadraticForm"二次形式
    "AutomorphismGroupOrder"自己同型群の階数
  • 命名関連特性
  • "AlternateNames"代替英語名
    "Name"英語名
    "Notation"表示用の一般的な表記
    "StandardName"Wolfram言語名
  • LatticeData[lattice,"Classes"]は，lattice が出現するクラスのリストを返す．
  • LatticeData["class"]は，指定クラスの名前付き格子のリストを返す．
  • LatticeData[lattice,"class"]は，lattice が指定のクラスのものかどうかによってTrueまたはFalseを返す．
  • 格子の基本クラス
  • "Even"偶数
    "Extremal"極値
    "Integral"積分
    "Odd"奇数格子
    "Unimodular"ユニモジュラ
  • 格子の負のクラス
  • "Nonextremal"非極値
    "Nonintegral"非積分
    "Nonunimodular"非ユニモジュラ
  • LatticeDataの使用にはインターネット接続が必要なことがある．

例題

すべて開くすべて閉じる

例  (3)

面心の立方格子：

面心の立方格子の基底：

六方最密格子の最小ベクトルに対応する点からのドロネーメッシュ：

スコープ  (24)

名前とクラス  (15)

非格子充填を含む古典的な名前の付いた格子を求める：

格子は標準的なWolfram言語名で指定することができる：

Barnes–Walll格子 は{"BarnesWall",n}で指定できる：

Bravais格子は格子が中央によった結晶系で指定できる：

整数格子：

積層格子：

Mordell–Weil格子 ：

ルート格子 ：

ルート格子 ：

ルート格子 ：

ルート格子には短い文字列形を使うことができる：

格子の英語名を求める：

代替名のリストも求めることができる：

クラスのリストを求める：

あるクラスに属する名前付き格子のリストを求める：

格子があるクラスに属するかどうかテストする：

格子が属するクラスのリストを得る：

偶数で積分である格子のリストを求める：

特性  (4)

使用可能な特性のリストを得る：

特定の格子に使用可能な特性のリストを得る：

三次元の格子には画像があるものがある：

表記を求める：

特性値  (5)

特性値は任意の有効なWolfram言語による式でよい：

属性"ThetaSeriesFunction"について，格子データは純関数として与えられる：

格子に適用不可の特性の値はMissing["NotApplicable"]になる：

格子に当てはまらない特性の値はMissing["NotAvailable"]になる：

格子の特性のリストを指定する：

一般化と拡張  (1)

LatticeDataは，四方充填のような非格子構造にも使うことができる：

アプリケーション  (3)

単位球面の格子点数：

半径の関数としての球上の格子点の数：

半径の関数としての球の中の格子点の数：

二次元格子の基底を返す：

格子の要素のいくつかを生成し表示する：

三次元格子の基底を与える：

格子の要素のいくつかを生成し表示する：

考えられる問題  (2)

格子の生成行列はSparseArrayとして返されることがある：

Normalを使って行列の式に変換する：

n 次格子を表すのに余分な座標が使われることがある：

Wolfram Research (2007), LatticeData, Wolfram言語関数， https://reference.wolfram.com/language/ref/LatticeData.html.

テキスト

Wolfram Research (2007), LatticeData, Wolfram言語関数， https://reference.wolfram.com/language/ref/LatticeData.html.

CMS

Wolfram Language. 2007. "LatticeData." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LatticeData.html.

APA

Wolfram Language. (2007). LatticeData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LatticeData.html

BibTeX

@misc{reference.wolfram_2024_latticedata, author="Wolfram Research", title="{LatticeData}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/LatticeData.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_latticedata, organization={Wolfram Research}, title={LatticeData}, year={2007}, url={https://reference.wolfram.com/language/ref/LatticeData.html}, note=[Accessed: 22-November-2024 ]}