Likelihood

Likelihood[dist,{x1,x2,…}]

分布 dist からの観察 x1, x2, …の尤度関数を与える．

Likelihood[proc,{{t1,x1},{t2,x2},…}]

時点 tiにおける過程 proc からの観察 xiについての尤度関数を与える．

Likelihood[proc,{path1,path2,…}]

過程 proc の path1, path2, … からの観察についての尤度関数を与える．

詳細

  • 尤度関数Likelihood[dist,{x1,x2,…}]は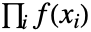で与えられる．ただし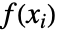，は xiにおける確率密度関数PDF[dist,xi]である．
  • スカラー値過程 proc については，尤度関数Likelihood[proc,{{t1,x1},{t2,x2},…}]は，Likelihood[SliceDistribution[proc,{t1,t2,…}],{{x1,x2,…}}]で与えられる．
  • ベクトル値過程 proc については，尤度関数Likelihood[proc,{{t1,{x1,…,z1},{t2,{x2,…,z2}},…}]は，Likelihood[SliceDistribution[proc,{t1,t2,…}],{{x1,…,z1,x2,…,z2,…}}]で与えられる．
  • 経路集合についての尤度関数Likelihood[proc,{path1,path2,…}]は，∏iLikelihood[proc,pathi]で与えられる．

例題

すべて開くすべて閉じる

例  (4)

正規分布の尤度関数を得る：

数値データの尤度を計算する：

尤度の等高線を と の関数として対数尺度でプロットする：

多変量データの尤度を計算する：

過程についての尤度を計算する：

スコープ  (12)

一変量パラメトリック分布  (2)

連続分布の尤度を計算する：

離散分布の尤度を計算する：

が未知であると仮定して尤度をプロットする：

多変量パラメトリック分布  (2)

母数が未知である連続多変量分布の対数尤度を得る：

を仮定して尤度曲面の対数を可視化する：

多変量離散分布について：

派生分布  (5)

切断標準正規分布の尤度を計算する：

構成分布の尤度を計算する：

尤度の等高線を下界と の関数として可視化する：

製品分布の尤度を計算する：

結果を独立した成分ごとの尤度の積として得る：

コピュラ分布の尤度を計算する：

尤度をカーネル母数の関数としてプロットする：

成分混合分布の尤度を計算する：

ランダム過程  (3)

連続パラメトリック過程の尤度を計算する：

スカラー値の離散パラメトリック過程の尤度を計算する：

過程母数の関数として尤度をプロットする：

スカラー値時系列過程の尤度を計算する：

ベクトル値時系列過程の尤度を計算する：

アプリケーション  (2)

閉形式のポアソン最尤推定法について解く：

最尤推定法を直接解く：

数値安定性についての対数尤度を使って最大化する：

尤度関数のプロット上で最適点にラベルを置く：

特性と関係  (4)

LikelihoodはデータのPDF値の積である：

Likelihoodの対数はLogLikelihoodである：

EstimatedDistributionは尤度を最大にして母数を推定する：

FindDistributionParametersは母数推定を規則として与える：

最適値近くの尤度関数を可視化する：

過程の尤度はそのスライス分布を使って計算することができる：

スライス分布を使う：

ベクトル値過程について：

スライス分布を使う：

時間スライス分布のLogLikelihoodで使うために，経路値をベクトル化する：

考えられる問題  (1)

連続パラメトリック過程の尤度は未定義であることがある：

これは，時点0における退化したスライス分布のためである：

正の時点から始める：

おもしろい例題  (2)

指数ベキ尤度について等値面を可視化する：

二変量正規尤度について等値面を可視化する：

Wolfram Research (2010), Likelihood, Wolfram言語関数， https://reference.wolfram.com/language/ref/Likelihood.html （2014年に更新）.

テキスト

Wolfram Research (2010), Likelihood, Wolfram言語関数， https://reference.wolfram.com/language/ref/Likelihood.html （2014年に更新）.

CMS

Wolfram Language. 2010. "Likelihood." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/Likelihood.html.

APA

Wolfram Language. (2010). Likelihood. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Likelihood.html

BibTeX

@misc{reference.wolfram_2024_likelihood, author="Wolfram Research", title="{Likelihood}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Likelihood.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_likelihood, organization={Wolfram Research}, title={Likelihood}, year={2014}, url={https://reference.wolfram.com/language/ref/Likelihood.html}, note=[Accessed: 22-November-2024 ]}