TransformationMatrix[tfun]
gives the homogeneous matrix associated with a TransformationFunction object.


TransformationMatrix
TransformationMatrix[tfun]
gives the homogeneous matrix associated with a TransformationFunction object.
Details
- For transformations in n dimensions, TransformationMatrix normally gives an
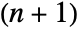 ×
×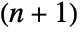 matrix.
matrix. - mat[[1;;n,1;;n]] gives the linear part of the transformation; mat[[1;;n,-1]] gives the displacement vector.
Examples
open all close allBasic Examples (1)
Scope (1)
Related Guides
History
Text
Wolfram Research (2007), TransformationMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/TransformationMatrix.html.
CMS
Wolfram Language. 2007. "TransformationMatrix." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TransformationMatrix.html.
APA
Wolfram Language. (2007). TransformationMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TransformationMatrix.html
BibTeX
@misc{reference.wolfram_2025_transformationmatrix, author="Wolfram Research", title="{TransformationMatrix}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/TransformationMatrix.html}", note=[Accessed: 26-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_transformationmatrix, organization={Wolfram Research}, title={TransformationMatrix}, year={2007}, url={https://reference.wolfram.com/language/ref/TransformationMatrix.html}, note=[Accessed: 26-February-2026]}