MandelbrotSetMemberQ

MandelbrotSetMemberQ[z]

returns True if z is in the Mandelbrot set, and False otherwise.

Details and Options

  • The Mandelbrot set is the set of all complex numbers 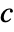for which the sequence 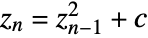does not diverge to infinity when starting with .
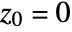  • With the option MaxIterations->n, the sequence 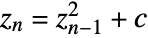will be iterated at most n times to determine if the sequence diverges.
  • The default setting is MaxIterations->1000.
  • If the maximum number of iterations is reached, z is assumed to be in the Mandelbrot set.

Examples

open allclose all

Basic Examples  (3)

Test whether is a member of the Mandelbrot set:

Zero is known to be inside the Mandelbrot set:

It takes a few hundred iterations to determine that 0.2501 is not in the Mandelbrot set:

Scope  (2)

MandelbrotSetMemberQ threads itself element-wise over lists:

MandelbrotSetMemberQ works on all kinds of numbers:

Options  (1)

MaxIterations  (1)

Sometimes MaxIterations needs to be increased to eliminate false positives:

Applications  (2)

Generate the Mandelbrot set from randomly chosen points:

Approximate the first point along the line that is not in the Mandelbrot set:

Show the point on the Mandelbrot set:

Possible Issues  (1)

With MaxIterations->Infinity, the calculation may not converge in a finite number of steps:

Neat Examples  (4)

MandelbrotSetMemberQ can be used to get an estimate of the area of the Mandelbrot set:

Display the Julia sets for points in the Mandelbrot set:

Rotate the Mandelbrot set:

Use MandelbrotSetMemberQ to distinguish Julia sets that are Cantor sets:

Wolfram Research (2014), MandelbrotSetMemberQ, Wolfram Language function, https://reference.wolfram.com/language/ref/MandelbrotSetMemberQ.html.

Text

Wolfram Research (2014), MandelbrotSetMemberQ, Wolfram Language function, https://reference.wolfram.com/language/ref/MandelbrotSetMemberQ.html.

CMS

Wolfram Language. 2014. "MandelbrotSetMemberQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MandelbrotSetMemberQ.html.

APA

Wolfram Language. (2014). MandelbrotSetMemberQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MandelbrotSetMemberQ.html

BibTeX

@misc{reference.wolfram_2025_mandelbrotsetmemberq, author="Wolfram Research", title="{MandelbrotSetMemberQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MandelbrotSetMemberQ.html}", note=[Accessed: 22-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_mandelbrotsetmemberq, organization={Wolfram Research}, title={MandelbrotSetMemberQ}, year={2014}, url={https://reference.wolfram.com/language/ref/MandelbrotSetMemberQ.html}, note=[Accessed: 22-February-2025 ]}