MarchenkoPasturDistribution[λ,σ]
漸近比 ![]() ,尺度母数
,尺度母数 ![]() のMarchenko–Pastur分布を表す.
のMarchenko–Pastur分布を表す.
MarchenkoPasturDistribution[λ]
単位尺度母数を持つMarchenko–Pastur分布を表す.


MarchenkoPasturDistribution
MarchenkoPasturDistribution[λ,σ]
漸近比 ![]() ,尺度母数
,尺度母数 ![]() のMarchenko–Pastur分布を表す.
のMarchenko–Pastur分布を表す.
MarchenkoPasturDistribution[λ]
単位尺度母数を持つMarchenko–Pastur分布を表す.
詳細
- MarchenkoPasturDistributionは,WishartMatrixDistributionからのランダム行列の極限的スペクトル密度である.
- Marchenko–Pastur分布の
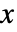 における累積分布関数の導関数は,
における累積分布関数の導関数は,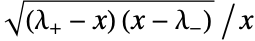 と比例する.ただし,
と比例する.ただし,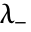 から
から 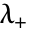 までで
までで 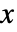 について
について 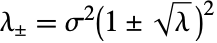 である.
である. - Marchenko–Pastur分布は
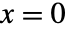 で点質量を持つ.その確率は,
で点質量を持つ.その確率は,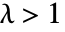 で
で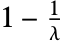 である.
である. - MarchenkoPasturDistributionでは,
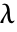 および
および 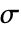 は任意の正の実数でよい.
は任意の正の実数でよい. - MarchenkoPasturDistributionでは,σ は任意の単位次元の数量でよく,λ は無次元量でよい. »
- MarchenkoPasturDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
例題
すべて開く すべて閉じるスコープ (7)
![]() でMarchenko–Pastur分布から擬似乱数のサンプルを生成する:
でMarchenko–Pastur分布から擬似乱数のサンプルを生成する:
そのヒストグラムをPDFと比較する:
![]() でMarchenko–Pastur分布から擬似乱数のサンプルを生成する:
でMarchenko–Pastur分布から擬似乱数のサンプルを生成する:
その累積ヒストグラムをCDFと比較する:
サンプルの累積ヒストグラムを推定分布のCDFと比較する:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (1)
MatrixPropertyDistributionを使って,恒等共分散を持つWishartランダム行列の固有値を表す:
スペクトル密度は,有限比 ![]() の大きい
の大きい ![]() と
と ![]() の極限において,MarchenkoPasturDistribution[λ]の確率密度関数に収束する:
の極限において,MarchenkoPasturDistribution[λ]の確率密度関数に収束する:
特性と関係 (3)
MarchenkoPasturDistributionは正の因子によるスケーリングの下で閉じている:
MarchenkoPasturDistributionは,![]() のときに0において原子量を持つ:
のときに0において原子量を持つ:
MarchenkoPasturDistributionは,Wishart行列の固有値の極限分布である.![]() における原子量はWishart行列が特異行列の場合に起る.恒等共分散を持つ特異Wishar行列を生成し,スケールされた固有値を計算する:
における原子量はWishart行列が特異行列の場合に起る.恒等共分散を持つ特異Wishar行列を生成し,スケールされた固有値を計算する:
MarchenkoPasturDistributionを固有値にフィットする:
固有値の累積ヒストグラムをCDFと比較する:
考えられる問題 (1)
![]() のMarchenko–Pastur分布は,連続的でも離散的でもない混合タイプの分布である:
のMarchenko–Pastur分布は,連続的でも離散的でもない混合タイプの分布である:
そのようなMarchenko–Pastur分布の累積密度関数は ![]() で不連続である:
で不連続である:
![]() のMarchenko–Pastur分布の確率密度関数は定義されず,PDFは未評価で返される:
のMarchenko–Pastur分布の確率密度関数は定義されず,PDFは未評価で返される:
テキスト
Wolfram Research (2015), MarchenkoPasturDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/MarchenkoPasturDistribution.html (2016年に更新).
CMS
Wolfram Language. 2015. "MarchenkoPasturDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/MarchenkoPasturDistribution.html.
APA
Wolfram Language. (2015). MarchenkoPasturDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MarchenkoPasturDistribution.html
BibTeX
@misc{reference.wolfram_2025_marchenkopasturdistribution, author="Wolfram Research", title="{MarchenkoPasturDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MarchenkoPasturDistribution.html}", note=[Accessed: 21-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_marchenkopasturdistribution, organization={Wolfram Research}, title={MarchenkoPasturDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/MarchenkoPasturDistribution.html}, note=[Accessed: 21-February-2026]}