MarchenkoPasturDistribution
MarchenkoPasturDistribution[λ,σ]
代表渐近比为 ![]() 且尺度参数为
且尺度参数为 ![]() 的 Marchenko–Pastur 分布.
的 Marchenko–Pastur 分布.
MarchenkoPasturDistribution[λ]
代表带单位尺度参数的 Marchenko–Pastur 分布.
更多信息

- MarchenkoPasturDistribution 是 WishartMatrixDistribution 中的随机矩阵的极限谱密度.
- Marchenko–Pastur 分布中
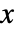 处的累积分布函数的导数和
处的累积分布函数的导数和 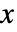 在
在 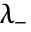 和
和 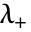 之间的
之间的 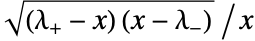 成比例,其中
成比例,其中 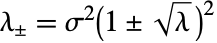 .
. - Marchenko–Pastur 分布在
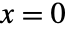 处有点质量,并且在
处有点质量,并且在 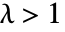 时概率为
时概率为 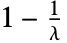 .
. - MarchenkoPasturDistribution 允许
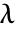 和
和 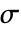 为任意正实数.
为任意正实数. - MarchenkoPasturDistribution 允许 σ 为任意单位量纲的量,而 λ 为一个无量纲的量. »
- MarchenkoPasturDistribution 可以和诸如 Mean、 CDF 和 RandomVariate 这样的函数一起使用.
范例
打开所有单元关闭所有单元范围 (7)
由 Marchenko–Pastur 分布在 ![]() 时生成一个伪随机数样本:
时生成一个伪随机数样本:
比较其直方图与 PDF:
由 Marchenko–Pastur 分布在 ![]() 时生成一个伪随机数样本:
时生成一个伪随机数样本:
比较其累积直方图与 CDF:
比较样本的累积直方图与估计分布的 CDF:
参数中对 Quantity 保持一致的使用将给出 QuantityDistribution:
应用 (1)
用 MatrixPropertyDistribution 表示有单位矩阵协方差的 Wishart 随机矩阵的特征值:
在有限比例 ![]() 的较大
的较大 ![]() 和
和 ![]() 的限制下,谱密度收敛于 MarchenkoPasturDistribution[λ] 的概率密度函数:
的限制下,谱密度收敛于 MarchenkoPasturDistribution[λ] 的概率密度函数:
属性和关系 (3)
MarchenkoPasturDistribution 在正因数缩放下封闭的:
![]() 时 MarchenkoPasturDistribution 在0处有原子量:
时 MarchenkoPasturDistribution 在0处有原子量:
MarchenkoPasturDistribution 是 Wishart 矩阵的特征值的极限分布. 原子量为 ![]() 出现在当 Wishart 矩阵是奇异矩阵时. 生成一个有单位矩阵协方差的奇异 Wishart 矩阵,计算比例特征值:
出现在当 Wishart 矩阵是奇异矩阵时. 生成一个有单位矩阵协方差的奇异 Wishart 矩阵,计算比例特征值:
拟合 MarchenkoPasturDistribution 至特征值:
比较特征值的累积直方图与 CDF:
可能存在的问题 (1)
Marchenko–Pastur 分布在 ![]() 时是一种混合型的分布,它既不是连续的,也不是离散的:
时是一种混合型的分布,它既不是连续的,也不是离散的:
这样的 Marchenko–Pastur 分布的累积分布函数在 ![]() 处是不连续的:
处是不连续的:
![]() 时Marchenko–Pastur 分布的概率密度函数是没有定义的,PDF 返回时没有进行计算:
时Marchenko–Pastur 分布的概率密度函数是没有定义的,PDF 返回时没有进行计算:
文本
Wolfram Research (2015),MarchenkoPasturDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MarchenkoPasturDistribution.html (更新于 2016 年).
CMS
Wolfram 语言. 2015. "MarchenkoPasturDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/MarchenkoPasturDistribution.html.
APA
Wolfram 语言. (2015). MarchenkoPasturDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MarchenkoPasturDistribution.html 年