MathieuGroupM23
散在型単純マシュー(Mathieu)群 ![]() を表す.
を表す.
予備知識
- MathieuGroupM23[]は,位数が
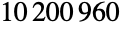 の群であるマシュー群
の群であるマシュー群 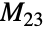 を表す.この群は,
位数が有限である26の散在型単純群の一つである.MathieuGroupM23のデフォルト表現は,2つの生成元を持つ点
を表す.この群は,
位数が有限である26の散在型単純群の一つである.MathieuGroupM23のデフォルト表現は,2つの生成元を持つ点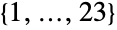 上の置換群としてのものである.
上の置換群としてのものである. - マシュー群
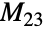 は散在型有限単純群で6番目に小さい.この群は,他の4つのマシュー群(MathieuGroupM11,MathieuGroupM12,MathieuGroupM22,MathieuGroupM24)とともに,数学者のÉmile Léonard Mathieuによって,散在型群としてはじめて,1800年代末に発見された.MathieuGroupM23は,MathieuGroupM22の元の一意的な任意の4タプル
は散在型有限単純群で6番目に小さい.この群は,他の4つのマシュー群(MathieuGroupM11,MathieuGroupM12,MathieuGroupM22,MathieuGroupM24)とともに,数学者のÉmile Léonard Mathieuによって,散在型群としてはじめて,1800年代末に発見された.MathieuGroupM23は,MathieuGroupM22の元の一意的な任意の4タプル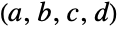 を他の任意の一意的な4タプル
を他の任意の一意的な4タプル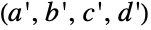 に写像する一意的な群の元
に写像する一意的な群の元 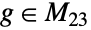 が少なくとも1つ存在するという意味で,4推移的である.
が少なくとも1つ存在するという意味で,4推移的である.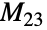 は,その置換表現に加え,生成元によって,
は,その置換表現に加え,生成元によって,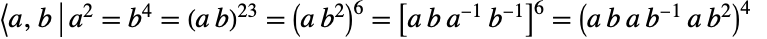
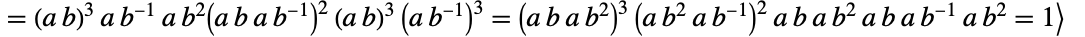 の関係として定義することができ,
の関係として定義することができ,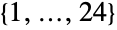 上で
上で 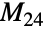 の点固定群でもある.マシュー群は,他の散在型単純群とともに,有限単純群の重要(かつ完全)な分類に大きく貢献した.
の点固定群でもある.マシュー群は,他の散在型単純群とともに,有限単純群の重要(かつ完全)な分類に大きく貢献した. - MathieuGroupM23[]には,GroupOrder,GroupGenerators,GroupElements等を含む通常の群論関数を適用することができる.マシュー群
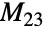 の数多くの計算済みの特性を,FiniteGroupData[{"Mathieu",23},"prop"]を介して得ることができる.
の数多くの計算済みの特性を,FiniteGroupData[{"Mathieu",23},"prop"]を介して得ることができる. - MathieuGroupM23は他の数多くのシンボルに関連している.MathieuGroupM23は集合的に散在型有限単純群の「第一世代」と呼ばれる5つの群の一つである(他にMathieuGroupM11,MathieuGroupM12,MathieuGroupM22,MathieuGroupM24がある).この群は,そのすべてがモンスター群のいわゆる部分商として現れる,「Happy」な20個の散在群の一つでもある.
例題
Wolfram Research (2010), MathieuGroupM23, Wolfram言語関数, https://reference.wolfram.com/language/ref/MathieuGroupM23.html.
テキスト
Wolfram Research (2010), MathieuGroupM23, Wolfram言語関数, https://reference.wolfram.com/language/ref/MathieuGroupM23.html.
CMS
Wolfram Language. 2010. "MathieuGroupM23." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MathieuGroupM23.html.
APA
Wolfram Language. (2010). MathieuGroupM23. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MathieuGroupM23.html