MellinConvolve

MellinConvolve[f,g,x,y]

式 f と g の x についてのメリン(Mellin)たたみ込みを与える．

MellinConvolve[f,g,{x1,x2,…},{y1,y2,…}]

多次元メリンたたみ込み与える．

詳細とオプション

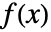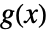  • 2つの関数 と のメリンたたみ込み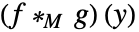は 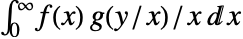で与えられる．
  • 2つの関数 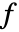と 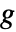の多次元メリンたたみ込みは 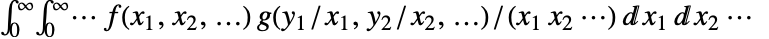で与えられる．
  • 使用可能なオプション
  • Assumptions $Assumptionsパラメータについての仮定
    GenerateConditions Falseパラメータについての条件を生成するかどうか
    MethodAutomatic使用するメソッド

例題

すべて開くすべて閉じる

例  (2)

2つの関数をたたみ込む：

多変量たたみ込みを行う：

スコープ  (8)

基本的な用法  (3)

記号的なパラメータ y についてのメリンたたみ込みを計算する：

パラメータについて厳密値を使う：

パラメータについて非厳密値を使う：

メリンたたみ込みが有効になる条件を得る：

パラメータについての仮定を指定する：

別の仮定を指定する：

一変量たたみ込み  (3)

初等関数：

特殊関数：

区分関数：

多変量たたみ込み  (2)

初等関数：

区分関数：

オプション  (2)

Assumptions  (1)

パラメータについての仮定を指定する：

GenerateConditions  (1)

メリンたたみ込みの有効性についての条件を指定する：

アプリケーション  (2)

2つの確率変数の積についてPDFを計算する：

MellinConvolveはこれらの確率変数の積についてのPDFを与える：

TransformedDistributionの結果と比較する：

積分 はパラメータ α に依存する．0から5までの間で積分を最大にする α の値を求める．与えられた積分は2関数のメリンたたみ込みであると考えられる：

f[x]と g[x]のメリンたたみ込みを計算する：

Integrateの結果と比較する：

積分を α の関数としてプロットする：

FindArgMaxを使って関数を0≤α≤5で最大にする引数を計算する：

特性と関係  (8)

MellinConvolveは積分 を計算する：

スケーリング：

可換性：

分配性：

DiracDeltaを使ったたたみ込み：

DiracDeltaの導関数：

たたみ込みのメリン変換は個々のメリン変換の積である：

MellinConvolveの y についての導関数：

MellinConvolve，MellinTransform，InverseMellinTransformの関係：

Wolfram Research (2016), MellinConvolve, Wolfram言語関数， https://reference.wolfram.com/language/ref/MellinConvolve.html.

テキスト

Wolfram Research (2016), MellinConvolve, Wolfram言語関数， https://reference.wolfram.com/language/ref/MellinConvolve.html.

CMS

Wolfram Language. 2016. "MellinConvolve." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MellinConvolve.html.

APA

Wolfram Language. (2016). MellinConvolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MellinConvolve.html

BibTeX

@misc{reference.wolfram_2024_mellinconvolve, author="Wolfram Research", title="{MellinConvolve}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/MellinConvolve.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mellinconvolve, organization={Wolfram Research}, title={MellinConvolve}, year={2016}, url={https://reference.wolfram.com/language/ref/MellinConvolve.html}, note=[Accessed: 22-November-2024 ]}