InverseMellinTransform[expr,s,x]
gives the inverse Mellin transform of expr.


InverseMellinTransform
InverseMellinTransform[expr,s,x]
gives the inverse Mellin transform of expr.
Details and Options

- The inverse Mellin transform of a function
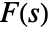 is defined to be
is defined to be 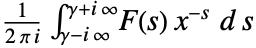
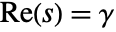 , lying in a strip
, lying in a strip 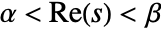 in which the function
in which the function 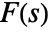 is holomorphic. In some cases, the strip of holomorphy may extend to a half-plane.
is holomorphic. In some cases, the strip of holomorphy may extend to a half-plane. - ConditionalExpression[expr,α<Re[s]<β] can be used to indicate the strip of holomorphy. »
- The following options can be given:
-
Assumptions $Assumptions assumptions on parameters GenerateConditions False whether to generate results that involve conditions on parameters Method Automatic what method to use - GenerateConditions can be used to obtain the strip of holomorphy. »
- Assumptions can be used to specify a strip of holomorphy. »
- If both Assumptions and ConditionalExpression are used to constrain the strip of holomorphy, then the intersection of the strips is used.
- In TraditionalForm, InverseMellinTransform is output using
![TemplateBox[{{F, (, s, )}, s, x}, InverseMellinTransform1] TemplateBox[{{F, (, s, )}, s, x}, InverseMellinTransform1]](Files/InverseMellinTransform.en/7.png) .
.
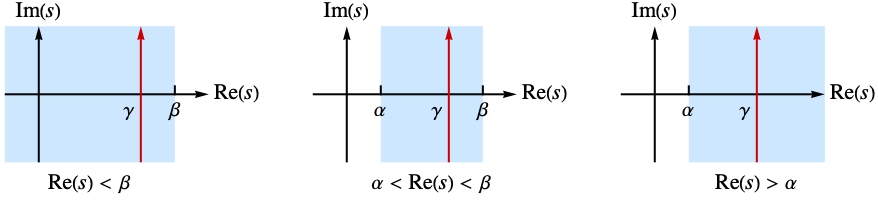
Examples
open all close allBasic Examples (2)
Compute the InverseMellinTransform of a function:
InverseMellinTransform for a product of functions:
Scope (10)
Basic Uses (4)
Compute the inverse Mellin transform of a function for a symbolic parameter x:
Use an exact value for the parameter:
Use an inexact value for the parameter:
Obtain the strip of holomorphy assumed by InverseMellinTransform:
TraditionalForm formatting:
Elementary Functions (3)
Options (2)
Assumptions (1)
The answer returned by InverseMellinTransform in this example is valid for Re[s]>0:
Use Assumptions to specify a different strip of holomorphy:
Use ConditionalExpression to specify the same assumptions:
GenerateConditions (1)
Obtain conditions for validity of the result in InverseMellinTransform:
GenerateConditions is set to False by default in this case:
Applications (2)
Evaluate ![]() , which may be regarded as a Mellin convolution of the following functions:
, which may be regarded as a Mellin convolution of the following functions:
Apply MellinTransform to each function:
Obtain the required integral by performing an inverse Mellin transform:
Compute the integral directly using Integrate:
Obtain the same result using MellinConvolve:
Find a particular solution for a differential equation using a Mellin transform technique:
Apply MellinTransform to the equation:
Solve for the Mellin transform:
Compute the required solution using InverseMellinTransform:
Obtain the solution using DSolveValue with a boundary condition at infinity:
Properties & Relations (4)
Use Asymptotic to compute an asymptotic approximation:
InverseMellinTransform and MellinTransform are mutual inverses:
Verify the relationship for a specific function:
InverseMellinTransform is a linear operator:
Possible Issues (2)
InverseMellinTransform may return different results depending on the assumptions:
In this example, the default answer is valid in a right half-plane:
The inverse Mellin transform may only exist for a certain range of values for x:
Related Guides
History
Text
Wolfram Research (2016), InverseMellinTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseMellinTransform.html.
CMS
Wolfram Language. 2016. "InverseMellinTransform." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseMellinTransform.html.
APA
Wolfram Language. (2016). InverseMellinTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseMellinTransform.html
BibTeX
@misc{reference.wolfram_2025_inversemellintransform, author="Wolfram Research", title="{InverseMellinTransform}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/InverseMellinTransform.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_inversemellintransform, organization={Wolfram Research}, title={InverseMellinTransform}, year={2016}, url={https://reference.wolfram.com/language/ref/InverseMellinTransform.html}, note=[Accessed: 10-March-2026]}