WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

MeyerWavelet[]

次数3のMeyerウェーブレットを表す．

MeyerWavelet[n]

等間隔の区間{-10,10}で評価された次数 n のMeyerウェーブレットを表す．

MeyerWavelet[n,lim]

等間隔の区間{-lim,lim}で評価された次数 n のウェーブレットを表す．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
基本的な用法  
ウェーブレット変換  
高次元  
特性と関係  
おもしろい例題  
関連項目
テクニカルノート
関連するガイド
履歴
引用書式

MeyerWavelet

MeyerWavelet[]

次数3のMeyerウェーブレットを表す．

MeyerWavelet[n]

等間隔の区間{-10,10}で評価された次数 n のMeyerウェーブレットを表す．

MeyerWavelet[n,lim]

等間隔の区間{-lim,lim}で評価された次数 n のウェーブレットを表す．

詳細

  • MeyerWaveletは正規直交ウェーブレット族を定義する．
  • MeyerWavelet[n]はMeyerWavelet[n,8]に等しい．
  • MeyerWavelet[n,lim]は任意の正の整数 n と実数の極限 lim について定義される．
  • スケーリング関数(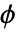)とウェーブレット関数(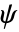)には無限サポートがある．これらの関数は対称である．
  • スケーリング関数(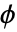)はそのフーリエ(Fourier)変換によって1 TemplateBox[{omega}, Abs]<=(2 pi)/3; cos(1/2 pi nu((3 TemplateBox[{omega}, Abs])/(2 pi)-1)) (2 pi)/3<=TemplateBox[{omega}, Abs]<=(4 pi)/3として与えられる． »
  • ウェーブレット関数(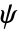)はそのフーリエ変換によってexp((ⅈ omega)/2) sin(pi/2 nu((3 TemplateBox[{omega}, Abs])/(2 pi)-1)) (2 pi)/3<=TemplateBox[{omega}, Abs]<=(4 pi)/3; exp((ⅈ omega)/2) cos(pi/2 nu((3 TemplateBox[{omega}, Abs])/(4 pi)-1)) (4 pi)/3<=TemplateBox[{omega}, Abs]<=(8 pi)/3として与えられる．
  • 多項式 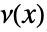は 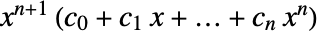の形式の多項式である．ただし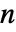， はMeyerウェーブレットの次数である．
  • MeyerWaveletはDiscreteWaveletTransformやWaveletPhi等の関数に使うことができる．

例題

すべて開く すべて閉じる

例  (3)

スケーリング関数：

Wolfram Language code: Plot[Evaluate[WaveletPhi[MeyerWavelet[3], x]], {x, -8, 8}, PlotRange -> All]
Wolfram Language code: WaveletPhi[MeyerWavelet[3], x]

ウェーブレット関数：

Wolfram Language code: Plot[Evaluate[WaveletPsi[MeyerWavelet[3], x]], {x, -8, 8}, PlotRange -> All]
Wolfram Language code: WaveletPsi[MeyerWavelet[3], x]

フィルタ係数：

Wolfram Language code: WaveletFilterCoefficients[MeyerWavelet[3, 5], {"PrimalLowpass", "PrimalHighpass"}]

スコープ  (9)

基本的な用法  (4)

主ローパスフィルタ係数を計算する：

Wolfram Language code: WaveletFilterCoefficients[MeyerWavelet[3], "PrimalLowpass"]

主ハイパスフィルタ係数：

Wolfram Language code: WaveletFilterCoefficients[MeyerWavelet[3], "PrimalHighpass"]

次数3のMeyerスケーリング関数：

Wolfram Language code: Plot[Evaluate[WaveletPhi[MeyerWavelet[3], x]], {x, -10, 10}, PlotRange -> All]

次数10のMeyerスケーリング関数：

Wolfram Language code: Plot[Evaluate[WaveletPhi[MeyerWavelet[10], x]], {x, -10, 10}, PlotRange -> All]

次数3のMeyerウェーブレット関数：

Wolfram Language code: Plot[Evaluate[WaveletPsi[MeyerWavelet[3], x]], {x, -10, 10}, PlotRange -> All]

次数10のMeyerウェーブレット関数：

Wolfram Language code: Plot[Evaluate[WaveletPsi[MeyerWavelet[10], x]], {x, -10, 10}, PlotRange -> All]

ウェーブレット変換  (4)

DiscreteWaveletTransformを計算する：

Wolfram Language code: data = Table[Sinc[x^2], {x, -3 π, 3 π, (6 π/1023)}];
Wolfram Language code: ListLinePlot[data, PlotRange -> All]
Wolfram Language code: dwt = DiscreteWaveletTransform[data, MeyerWavelet[3, 12], 2]

ウェーブレット係数の木を見る：

Wolfram Language code: dwt["TreeView"]

ウェーブレット係数の次元を得る：

Wolfram Language code: dwt["Dimensions"]

ウェーブレット係数をプロットする：

Wolfram Language code: WaveletListPlot[dwt, PlotLayout -> "CommonXAxis"]

MeyerWaveletを使ってDiscreteWaveletPacketTransformを行うことができる：

Wolfram Language code: data = Table[Sinc[t^2], {t, -3 π, 3 π, (6 π/1023)}];
Wolfram Language code: dwpt = DiscreteWaveletPacketTransform[data, MeyerWavelet[3, 12], 2]

ウェーブレット係数の木を見る：

Wolfram Language code: dwpt["TreeView"]

ウェーブレット係数の次元を得る：

Wolfram Language code: dwpt["Dimensions"]

ウェーブレット係数をプロットする：

Wolfram Language code: WaveletListPlot[dwpt, PlotLayout -> "CommonXAxis"]

MeyerWaveletを使ってStationaryWaveletTransformを行うことができる：

Wolfram Language code: data = Table[Sinc[t^2], {t, -3 π, 3 π, (6 π/1023)}];
Wolfram Language code: swt = StationaryWaveletTransform[data, MeyerWavelet[3, 12], 2];

ウェーブレット係数の木を見る：

Wolfram Language code: swt["TreeView"]

ウェーブレット係数の次元を得る：

Wolfram Language code: swt["Dimensions"]

ウェーブレット係数をプロットする：

Wolfram Language code: WaveletListPlot[swt, PlotLayout -> "CommonXAxis"]

MeyerWaveletを使ってStationaryWaveletPacketTransformを行うことができる：

Wolfram Language code: data = Table[Sinc[t^2], {t, -3 π, 3 π, (6 π/1023)}];
Wolfram Language code: swpt = StationaryWaveletPacketTransform[data, MeyerWavelet[3, 12], 2];

ウェーブレット係数の木を見る：

Wolfram Language code: swpt["TreeView"]

ウェーブレット係数の次元を得る：

Wolfram Language code: swpt["Dimensions"]

ウェーブレット係数をプロットする：

Wolfram Language code: WaveletListPlot[swpt, PlotLayout -> "CommonXAxis"]

高次元  (1)

多変量スケーリング関数と多変量ウェーブレット関数はそれぞれその一変量関数の積である：

Wolfram Language code: ϕ = WaveletPhi[MeyerWavelet[3, 8]]; ψ = WaveletPsi[MeyerWavelet[3, 8]];
Wolfram Language code: Plot3D[Evaluate[ϕ[x] ψ[y]], {x, -8, 8}, {y, -8, 8}, PlotRange -> All, ColorFunction -> "SolarColors", Mesh -> None, Axes -> None]
Wolfram Language code: Plot3D[Evaluate[ϕ[x] ψ[y]], {x, -8, 8}, {y, -8, 8}, PlotRange -> All, ColorFunction -> "SolarColors", Mesh -> None, Axes -> None]
Wolfram Language code: Plot3D[Evaluate[ψ[x] ϕ[y]], {x, -8, 8}, {y, -8, 8}, PlotRange -> All, ColorFunction -> "SolarColors", Mesh -> None, Axes -> None]
Wolfram Language code: Plot3D[Evaluate[ψ[x] ψ[y]], {x, -8, 8}, {y, -8, 8}, PlotRange -> All, ColorFunction -> "SolarColors", Mesh -> None, Axes -> None]

特性と関係  (10)

ローパスフィルタ係数の総和は単位元にほぼ等しい．：

Wolfram Language code: Chop[Total[WaveletFilterCoefficients[MeyerWavelet[3, 20], "PrimalLowpass"][[All, 2]]]]

ハイパスフィルタ係数の総和は0にほぼ等しい．：

Wolfram Language code: Chop[Total[WaveletFilterCoefficients[MeyerWavelet[3, 20], "PrimalHighpass"][[All, 2]]]]

スケーリング関数を積分すると単位元になる．：

Wolfram Language code: ϕ = WaveletPhi[MeyerWavelet[3]];
Wolfram Language code: Subsuperscript[∫, -∞, ∞]ϕ[x]ⅆx

ウェーブレット関数を積分すると0になる．：

Wolfram Language code: ψ = WaveletPsi[MeyerWavelet[3, 20]];
Wolfram Language code: NIntegrate[ψ[x], {x, -∞, ∞}]

は再帰方程式 を満足する：

Wolfram Language code: ϕ = WaveletPhi[MeyerWavelet[3]];
Wolfram Language code: a = WaveletFilterCoefficients[MeyerWavelet[3], "PrimalLowpass"];

要素と再帰の総和をプロットする：

Wolfram Language code: scalet[x_, ϕ_, a_] := 2 Table[a[[i, 2]] ϕ[2 x - a[[i, 1]]], {i, Length[a]}]
Wolfram Language code: {Plot[Evaluate[scalet[x, ϕ, a]], {x, -8, 8}, PlotRange -> All], Plot[Total[scalet[x, ϕ, a]], {x, -8, 8}, PlotRange -> All]}

は再帰方程式 を満足する：

Wolfram Language code: ϕ = WaveletPhi[MeyerWavelet[3]];
Wolfram Language code: b = WaveletFilterCoefficients[MeyerWavelet[3], "PrimalHighpass"];

要素と再帰の総和をプロットする：

Wolfram Language code: wavelet[x_, ϕ_, b_] := 2 Table[b[[i, 2]] ϕ[2 x - b[[i, 1]]], {i, Length[b]}]
Wolfram Language code: {Plot[Evaluate[wavelet[x, ϕ, b]], {x, -8, 8}, PlotRange -> All], Plot[Total[wavelet[x, ϕ, b]], {x, -8, 8}, PlotRange -> All]}

の周波数応答は で与えられる：

Wolfram Language code: h[wav_, ω_] := With[{a = WaveletFilterCoefficients[wav]}, Underoverscript[∑, i, Length[a]]a[[i, 2]] Exp[-I a[[i, 1]] ω]]

フィルタはローパスフィルタである：

Wolfram Language code: Plot[Evaluate[Abs[h[MeyerWavelet[3, 20], ω]]], {ω, -π, π}, Ticks -> {{-π, -(π/2), 0, (π/2), π}, Automatic}, AxesLabel -> {ω, Abs[H[ω]]}]

の周波数応答はで与えられる：

Wolfram Language code: g[wav_, ω_] := With[{b = WaveletFilterCoefficients[wav, "PrimalHighpass"]}, Underoverscript[∑, i, Length[b]]b[[i, 2]] Exp[-I b[[i, 1]] ω]]

フィルタはハイパスフィルタである：

Wolfram Language code: Plot[Evaluate[Abs[g[MeyerWavelet[3, 20], ω]]], {ω, -π, π}, Ticks -> {{-π, -(π/2), 0, (π/2), π}, Automatic}, AxesLabel -> {ω, Abs[G[ω]]}]

のフーリエ変換はで与えられる：

Wolfram Language code: h[wav_, ω_] := With[{a = WaveletFilterCoefficients[wav]}, Underoverscript[∑, i, Length[a]]a[[i, 2]] Exp[-I a[[i, 1]] ω]]
Wolfram Language code: fh[wav_, ω_, j_] := Abs[Underoverscript[∏, i, j]h[wav, (ω/2^i)]]
Wolfram Language code: Plot[Evaluate[fh[MeyerWavelet[3, 20], ω, 10]], {ω, -2 π, 2 π}, PlotRange -> All, Ticks -> {Range[-2 π, 2 π, (2 π/3)], {1}}, AxesLabel -> {ω, Overscript[ϕ, ^ ][ω]}]

上記の結果を厳密なフーリエ変換と比較する：

Wolfram Language code: phihat[n_, ω_] := Piecewise[{{1, Abs[ω] ≤ (2 π/3)}, {Cos[(1/2) π ν[n, (3 Abs[ω]/2 π) - 1]], (2 π/3) ≤ Abs[ω] ≤ (4 π/3)}}]
Wolfram Language code: νcoeff[n_, l_] := (Underoverscript[∑, k = Ceiling[(l - 1/2)], n]((Binomial[n, k] Binomial[2 k + 1, l] 2^l (-1)^k + l - 1) (2 n + 1)!!/2 k + 1)/2 (2 n)!!)
Wolfram Language code: ν[n_, x_] := Piecewise[{{0, x ≤ 0}, {Underoverscript[∑, l = n + 1, 2 n + 1]νcoeff[n, l] x^l, 0 ≤ x ≤ 1}, {1, x ≥ 1}}]
Wolfram Language code: Plot[Abs[phihat[3, ω]], {ω, -2 π, 2 π}, PlotRange -> All, AxesLabel -> {ω, Overscript[ϕ, ^ ][ω]}, Ticks -> {Range[-2 π, 2 π, (2 π/3)], {1}}]

のフーリエ変換は で与えられる：

Wolfram Language code: h[wav_, ω_] := With[{a = WaveletFilterCoefficients[wav]}, Underoverscript[∑, i, Length[a]]a[[i, 2]] Exp[-I a[[i, 1]] ω]]
Wolfram Language code: g[wav_, ω_] := With[{b = WaveletFilterCoefficients[wav, "PrimalHighpass"]}, Underoverscript[∑, i, Length[b]]b[[i, 2]] Exp[-I b[[i, 1]] ω]]
Wolfram Language code: fg[wav_, ω_, j_] := Abs[g[wav, (ω/2)] Underoverscript[∏, i = 2, j]h[wav, (ω/2^i)]]
Wolfram Language code: Plot[Evaluate[fg[MeyerWavelet[3, 20], ω, 10]], {ω, -10, 10}, PlotRange -> All, AxesLabel -> {ω, Abs[Overscript[ψ, ^ ][ω]]}]

上記の結果を厳密なフーリエ変換と比較する：

Wolfram Language code: phihat[n_, ω_] := Piecewise[{{1, Abs[ω] ≤ (2 π/3)}, {Cos[(1/2) π ν[n, (3 Abs[ω]/2 π) - 1]], (2 π/3) ≤ Abs[ω] ≤ (4 π/3)}}]
Wolfram Language code: νcoeff[n_, l_] := (Underoverscript[∑, k = Ceiling[(l - 1/2)], n]((Binomial[n, k] Binomial[2 k + 1, l] 2^l (-1)^k + l - 1) (2 n + 1)!!/2 k + 1)/2 (2 n)!!)
Wolfram Language code: ν[n_, x_] := Piecewise[{{0, x ≤ 0}, {Underoverscript[∑, l = n + 1, 2 n + 1]νcoeff[n, l] x^l, 0 ≤ x ≤ 1}, {1, x ≥ 1}}]
Wolfram Language code: psihat[n_Integer, w_] := Exp[(I w/2)] (phihat[n, w + 2 π] + phihat[n, w - 2 π]) phihat[n, (w/2)]
Wolfram Language code: Plot[Abs[psihat[3, ω]], {ω, -10, 10}, PlotRange -> All, AxesLabel -> {ω, Abs[Overscript[ψ, ^ ][ω]]}]

おもしろい例題  (2)

スケーリング関数の平行移動と膨張をプロットする：

Wolfram Language code: ϕ[x_, j_, k_] := 2^j / 2 WaveletPhi[MeyerWavelet[3], 2^j x - k]
Wolfram Language code: Plot[Evaluate[Table[ϕ[x, j, 0], {j, 0, 2}]], {x, -1, 1}, Filling -> Axis, PlotRange -> All]
Wolfram Language code: Plot[Evaluate[Table[ϕ[x, 2, k], {k, 0, 2^2 - 1}]], {x, -1, 2}, Filling -> Axis, PlotRange -> All]

ウェーブレット関数の平行移動と膨張をプロットする：

Wolfram Language code: ψ[x_, j_, k_] := 2^j / 2 WaveletPsi[MeyerWavelet[3], 2^j x - k]
Wolfram Language code: Plot[Evaluate[Table[ψ[x, j, 0], {j, 0, 2}]], {x, -0.5, 1}, Filling -> Axis, PlotRange -> All]
Wolfram Language code: Plot[Evaluate[Table[ψ[x, 2, k], {k, 0, 2^2 - 1}]], {x, -0.5, 1.5}, Filling -> Axis, PlotRange -> All]
Wolfram Research (2010), MeyerWavelet, Wolfram言語関数， https://reference.wolfram.com/language/ref/MeyerWavelet.html.

テキスト

Wolfram Research (2010), MeyerWavelet, Wolfram言語関数， https://reference.wolfram.com/language/ref/MeyerWavelet.html.

CMS

Wolfram Language. 2010. "MeyerWavelet." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MeyerWavelet.html.

APA

Wolfram Language. (2010). MeyerWavelet. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MeyerWavelet.html

BibTeX

@misc{reference.wolfram_2026_meyerwavelet, author="Wolfram Research", title="{MeyerWavelet}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/MeyerWavelet.html}", note=[Accessed: 03-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_meyerwavelet, organization={Wolfram Research}, title={MeyerWavelet}, year={2010}, url={https://reference.wolfram.com/language/ref/MeyerWavelet.html}, note=[Accessed: 03-November-2026]}