WaveletPhi[wave,x]
gives the scaling function ![]() for the symbolic wavelet wave evaluated at x.
for the symbolic wavelet wave evaluated at x.
WaveletPhi[wave]
gives the scaling function as a pure function.


WaveletPhi
WaveletPhi[wave,x]
gives the scaling function ![]() for the symbolic wavelet wave evaluated at x.
for the symbolic wavelet wave evaluated at x.
WaveletPhi[wave]
gives the scaling function as a pure function.
Details and Options

- The scaling function
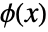 satisfies the recursion equation
satisfies the recursion equation 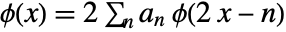 , where
, where 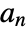 are the lowpass filter coefficients.
are the lowpass filter coefficients. - WaveletPhi[wave,x,"Dual"] gives the dual scaling function
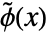 for biorthogonal wavelets such as BiorthogonalSplineWavelet and ReverseBiorthogonalSplineWavelet.
for biorthogonal wavelets such as BiorthogonalSplineWavelet and ReverseBiorthogonalSplineWavelet. - The dual scaling function satisfies the recursion equation
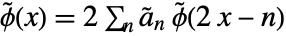 , where
, where 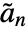 are the dual lowpass filter coefficients.
are the dual lowpass filter coefficients. - The following options can be used:
-
MaxRecursion 8 number of recursive iterations to use WorkingPrecision MachinePrecision precision to use in internal computations
Examples
open all close allScope (4)
Compute primal scaling function:
Scaling function ![]() for HaarWavelet:
for HaarWavelet:
ReverseBiorthogonalSplineWavelet:
Multivariate scaling and wavelet functions are products of univariate ones:
Options (3)
WorkingPrecision (2)
Properties & Relations (4)
Related Guides
History
Text
Wolfram Research (2010), WaveletPhi, Wolfram Language function, https://reference.wolfram.com/language/ref/WaveletPhi.html.
CMS
Wolfram Language. 2010. "WaveletPhi." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletPhi.html.
APA
Wolfram Language. (2010). WaveletPhi. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WaveletPhi.html
BibTeX
@misc{reference.wolfram_2025_waveletphi, author="Wolfram Research", title="{WaveletPhi}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WaveletPhi.html}", note=[Accessed: 17-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_waveletphi, organization={Wolfram Research}, title={WaveletPhi}, year={2010}, url={https://reference.wolfram.com/language/ref/WaveletPhi.html}, note=[Accessed: 17-January-2026]}