WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

NormalizationLayer[]

二次元目以降の次元の入力データを正規化し，独立したスケールとバイアスを一次元の各成分に適用する，訓練可能なネット層を表す．

NormalizationLayer[aggregationlevels]

指定された集約レベルでデータを正規化し，学習したスケールとバイアスを残りのレベルに適用する．

NormalizationLayer[aggregationlevels,scalinglevels]

学習したスケールとバイアスを指定されたスケールレベルに適用する．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
オプション  
"Biases"  
"Epsilon"  
"GroupNumber"  
Method  
"Scaling"  
"Unbiased"  
特性と関係  
考えられる問題  
関連項目
テクニカルノート
関連するガイド
履歴
引用書式

NormalizationLayer

NormalizationLayer[]

二次元目以降の次元の入力データを正規化し，独立したスケールとバイアスを一次元の各成分に適用する，訓練可能なネット層を表す．

NormalizationLayer[aggregationlevels]

指定された集約レベルでデータを正規化し，学習したスケールとバイアスを残りのレベルに適用する．

NormalizationLayer[aggregationlevels,scalinglevels]

学習したスケールとバイアスを指定されたスケールレベルに適用する．

詳細とオプション

  • NormalizationLayerはデータの正規化に使われる．その後には学習可能なアフィン変換が続く．
  • aggregationlevels は，平均と分散統計の計算に入力のどのレベルを集約するかを決定する．scalinglevels は，入力のどのレベルにコンポーネントごとの特定のスケーリング値とバイアスを適用するかを決定する．
  • 次は，aggregationlevels の可能な値である．
  • aレベル a のみを集約
    a1;;a2レベル a1からレベル a2までを集約
    {a1,…}レベル aiを集約
  • デフォルトの集約レベルは2;;Allである．
  • 次は，scalinglevels の可能な値である．
  • "Complement"集約レベルを除いた全レベル（デフォルト）
    "Same"集約レベルと同じレベル
    sレベル i のみ
    s1;;s2レベル s1からレベル s2まで
    {s1,…}レベル si
  • 次の選択的パラメータを含めることができる．
  • "Epsilon" 0.001安定性パラメータ
    "GroupNumber" Noneデータをグループに分割するかどうか
    LearningRateMultipliersAutomaticスケーリングおよび／またはバイアスパラメータの学習率乗数
    "Unbiased" False（長さの代りに）長さ-1で標準偏差を正規化するかどうか
    Method "Standardize"使用する正規化メソッド
  • 次は，Methodの可能な設定である．
  • "RMS"二乗平均平方根を使うxi/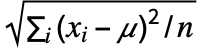
    "Standardize"Standardizeを使う(xi-μ)/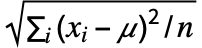
  • 集約レベル{a1,…,an}のとき，"GroupNumber"{g1,…,gn}と設定すると，ajレベルが gjグループに分割され，個別に正規化される．レベル ajの次元は gjの整数倍でなければならない．
  • 次の学習可能パラメータを指定することができる．
  • "Biases"Automatic学習可能なバイアスパラメータ
    "Scaling"Automatic学習可能なスケールパラメータ
  • Automatic設定の場合は，NetInitializeまたはNetTrainが使われるとスケールパラメータとバイアスパラメータが自動的に初期化される．Noneの設定の場合は，スケールと追加のバイアスを無効にすることができる．
  • スケールとバイアスの両パラメータが初期化あるいは無効にされると，NormalizationLayer[…][input]は層を適用した結果から明示的に出力を計算する，
  • NormalizationLayer[…][input]は，層を input に適用した結果の出力を明示的に計算する．
  • NormalizationLayer[…][{input1,input2,…}]は各 inputiの出力を明示的に計算する．
  • より大きいネット内の他の層から推測できない場合は，オプション"Input"->{d1,d2,…}を使ってNormalizationLayerの入力次元を固定することができる．
  • NetExtractを使って，スケール，バイアス，イプシロンの各パラメータをNormalizationLayerオブジェクトから抽出することができる．
  • NormalizationLayerは，NetChain，NetGraph等の内部で使われることが多い．
  • NormalizationLayerはNetGraph等で使うために次のポートを開放する．
  • "Input"1階より上の配列
    "Output"1階より上の配列
  • 集約レベル{a,b,…}では da×db×…の部分配列 xAに，スケールレベル{i,j,…}では di×dj×…の部分配列 xIに分解できる，入力配列 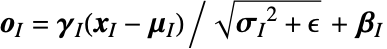について考える．スケールパラメータ 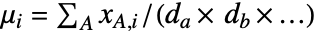とバイアスパラメータ 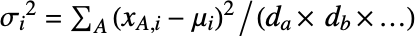の次元は(di×dj×…)である．
  • "Standardize"メソッドの出力は 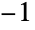を介して入手できる．ただし，平均配列は 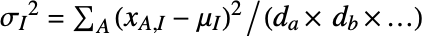によって，偏差は 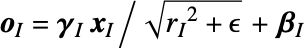によって与えられる．
  • "RMS"メソッドの出力は 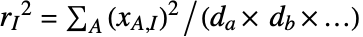を介して入手できる．ただし，RMS配列は 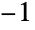によって与えられる．
  • 出力は常に入力と同じ次元である．
  • デフォルトのNormalizationLayer[]は，Ulyanov et al.による2016年の「Instance Normalization: The Missing Ingredient for Fast Stylization」における一次元のチャンネルレベルと続くレベルの空間次元を持つ正規化の例に対応する．
  • Method"RMS"を使ってZhang et al.による2019年の「Root Mean Square Layer Normalization」にあるRMSNormが再作成できる． »
  • NormalizationLayer[2;;All,"Same","Input"{n,Automatic}]は，Ba et al.による2016年の「Layer Normalization」における最終レベルのチャンネル次元と一次元のチャンネルレベルにおける時間次元の正規化の例に対応する．
  • NormalizationLayer[All,1,"GroupNumber"{n,1,1,…},"Input"{m*n,…}]は，Wu et al.による2018年の群の正規化についての「Group Normalization」における一次元のチャンネルレベルと続くレベルの空間次元を持つ正規化の例に対応する．
  • Options[NormalizationLayer]は層を構築する際のデフォルトオプションのリストを与える．Options[NormalizationLayer[…]]はデータについて層を評価する際のデフォルトオプションのリストを与える．
  • Information[NormalizationLayer[…]]は層についてのレポートを与える．
  • Information[NormalizationLayer[…],prop]はNormalizationLayer[…]の特性 prop の値を与える．使用可能な特性はNetGraphと同じである．

例題

すべて開く すべて閉じる

例  (2)

NormalizationLayerを作る：

Wolfram Language code: NormalizationLayer[]

階数3の配列を取る，初期化されたNormalizationLayerを作る：

Wolfram Language code: norm = NetInitialize@NormalizationLayer["Input" -> {2, 2, 3}]

この層を入力に適用する：

Wolfram Language code: MatrixForm /@ norm[{{{1, 2, 3}, {4, 5, 6}}, {{3, 2, 1}, {1, 2, 3}}}]

スコープ  (3)

RGB画像を取り込んでRGB画像を返す正規化層の例を作る：

Wolfram Language code: instancenorm = NetInitialize@NormalizationLayer["Input" -> NetEncoder["Image"], "Output" -> NetDecoder["Image"]]

この層を画像に適用する：

Wolfram Language code: instancenorm[[image]]

NormalizationLayerは自動的に入力バッチに縫い込まれる：

Wolfram Language code: instancenorm[{[image], [image]}]

二次元ベクトルの列を取り込んで，2倍にスケールされてシフトされた正規化ベクトルの列を返すNormalizationLayerを作る：

Wolfram Language code: layernorm = NormalizationLayer[2, "Same", "Input" -> {"Varying", 2}, "Scaling" -> 2, "Biases" -> -1]

層正規化を正弦波入力に適用する：

Wolfram Language code: input = Table[Cos[x * s] * x, {x, Range[0, 1, 0.01]}, {s, {2 * Pi, 4 * Pi}}];
Wolfram Language code: output = layernorm[input];

正規化の前と後の値を可視化する：

Wolfram Language code: ListLinePlot[Transpose@input]
Wolfram Language code: ListLinePlot[Transpose@output]

階数6の配列を取り入れて全次元について正規化する，初期化されたNormalizationLayerを作る：

Wolfram Language code: norm = NetInitialize@NormalizationLayer[All, "Same", "Input" -> {1, 2, 3, 4, 5, 6}]

この層を入力に適用する：

Wolfram Language code: Mean@Flatten@norm[RandomReal[1, {1, 2, 3, 4, 5, 6}]]
Wolfram Language code: StandardDeviation@Flatten@norm[RandomReal[1, {1, 2, 3, 4, 5, 6}]]

オプション  (9)

"Biases"  (2)

バイアスを明示的に指定してNormalizationLayerを作る：

Wolfram Language code: norm = NormalizationLayer["Biases" -> {2.1, 3.4}]

バイアスを抽出する：

Wolfram Language code: NetExtract[norm, "Biases"]

バイアスなしでNormalizationLayerを作る：

Wolfram Language code: norm = NormalizationLayer["Biases" -> None]

この層は学習可能なバイアスを持たない：

Wolfram Language code: NetExtract[norm, "Biases"]

"Epsilon"  (1)

"Epsilon"パラメータを明示的に指定してNormalizationLayerを作る：

Wolfram Language code: norm = NormalizationLayer["Epsilon" -> 0.1]

"Epsilon"パラメータを抽出する：

Wolfram Language code: NetExtract[norm, "Epsilon"]

"GroupNumber"  (2)

NormalizationLayerは，集約レベル全体の分散と平均を計算する：

Wolfram Language code: norm = NormalizationLayer["Biases" -> None, "Scaling" -> None]
Wolfram Language code: data = {{0.26, 0.8, 0.8, 0.08}, {0.74, 0.72, 0.66, 0.94}, {0.3, 0.4, 0.52, 0.4}};
Wolfram Language code: norm[data]//MatrixForm

集約レベルを2つのグループに分割するように指定する：

Wolfram Language code: groups = 2;
Wolfram Language code: normG = NetInitialize@NormalizationLayer["GroupNumber" -> {groups}, "Biases" -> None, "Scaling" -> None]

それぞれのグループが個別に正規化される：

Wolfram Language code: normG[data]//MatrixForm

これは正規化の前に入力を再形成することに等しい：

Wolfram Language code: reshaped = ArrayReshape[data, {3, groups, 4 / groups}]

1レベル深く正規化を適用することと組み合せる：

Wolfram Language code: norm2 = NormalizationLayer[3, "Biases" -> None, "Scaling" -> None];
Wolfram Language code: ArrayReshape[norm2[reshaped], {3, 4}]//MatrixForm

スケーリングなしでNormalizationLayerを作成する：

Wolfram Language code: norm = NormalizationLayer["Scaling" -> None, "Biases" -> None]

この層には学習可能なスケーリングパラメータがない：

Wolfram Language code: NetExtract[norm, "Scaling"]

Method  (1)

Zhang et al.の「Root Mean Square Layer Normalization」からRMSNorm層を作成する：

Wolfram Language code: norm = NormalizationLayer[2 ;; All, "Same", Method -> "RMS", "Input" -> {"n", Automatic}]

"Scaling"  (2)

スケールパラメータを明示的に指定してNormalizationLayerを作る：

Wolfram Language code: norm = NormalizationLayer["Scaling" -> {-1.2, 2.3, 4.5}]

スケールパラメータを抽出する：

Wolfram Language code: NetExtract[norm, "Scaling"]

スケールなしでNormalizationLayerを作る：

Wolfram Language code: norm = NormalizationLayer["Scaling" -> None, "Biases" -> None]

この層は学習可能なスケールパラメータを持たない：

Wolfram Language code: NetExtract[norm, "Scaling"]

"Unbiased"  (1)

デフォルトの分散推定器は，通常，ニューラルネットアプリケーションでは偏っている：

Wolfram Language code: norm = NormalizationLayer["Biases" -> None, "Scaling" -> None, "Epsilon" -> 0]
Wolfram Language code: data = {{0.78, 0.4}, {0.16, 0.52}, {0.39, 0.19}};
Wolfram Language code: norm[data]

これは以下に等しい：

Wolfram Language code: (# - Mean[#]) / Sqrt@Mean[(# - Mean[#]) ^ 2]& /@ data

NormalizationLayerを偏りがない分散推定器で定義する：

Wolfram Language code: normUnbiased = NormalizationLayer["Biases" -> None, "Scaling" -> None, "Epsilon" -> 0, "Unbiased" -> True]
Wolfram Language code: normUnbiased[{{0.78, 0.4}, {0.16, 0.52}, {0.39, 0.19}}]

分散の計算は，これでVarianceと等しくなった：

Wolfram Language code: (# - Mean[#]) / Sqrt@Variance[#]& /@ data

特性と関係  (1)

NormalizationLayerは，一般に，Standardizeとは等しくない：

Wolfram Language code: norm = NormalizationLayer["Input" -> {3, 2}]

単位"Scaling"とゼロ"Biases"で層を初期化する：

Wolfram Language code: norm = NetInitialize[norm]

データの標準化を計算する：

Wolfram Language code: data = {{0.609572, 0.583343}, {0.475967, 0.762314}, {0.598652, 0.357806}};
Wolfram Language code: Standardize /@ data//MatrixForm

安定性パラメータとバイアスのある分散推定器は違いを導入する：

Wolfram Language code: norm[data]//MatrixForm

NormalizationLayer遠正規化なしで定義する：

Wolfram Language code: norm2 = NetInitialize@NormalizationLayer["Input" -> {3, 2}, "Epsilon" -> 0, "Unbiased" -> True]

結果はStandardizeに近い：

Wolfram Language code: norm2[data]//MatrixForm

考えられる問題  (1)

NormalizationLayerは，その全入出力次元が既知になるまで初期化できない：

Wolfram Language code: NetInitialize@NormalizationLayer[]
Wolfram Language code: NetInitialize@NormalizationLayer["Input" -> {2, 55, 55}]
Wolfram Research (2019), NormalizationLayer, Wolfram言語関数， https://reference.wolfram.com/language/ref/NormalizationLayer.html （2025年に更新）.

テキスト

Wolfram Research (2019), NormalizationLayer, Wolfram言語関数， https://reference.wolfram.com/language/ref/NormalizationLayer.html （2025年に更新）.

CMS

Wolfram Language. 2019. "NormalizationLayer." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/NormalizationLayer.html.

APA

Wolfram Language. (2019). NormalizationLayer. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NormalizationLayer.html

BibTeX

@misc{reference.wolfram_2026_normalizationlayer, author="Wolfram Research", title="{NormalizationLayer}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/NormalizationLayer.html}", note=[Accessed: 18-June-2026]}

BibLaTeX

@online{reference.wolfram_2026_normalizationlayer, organization={Wolfram Research}, title={NormalizationLayer}, year={2025}, url={https://reference.wolfram.com/language/ref/NormalizationLayer.html}, note=[Accessed: 18-June-2026]}