NumberFieldSignature

NumberFieldSignature[a]

gives the signature of the field generated by the algebraic number a.

Details

  • NumberFieldSignature[a] gives a list 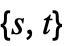{s,t} of the number of real roots and the number of pairs of conjugate roots for the minimal polynomial of a.

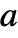Examples

open allclose all

Basic Examples  (2)

Find the signature of the number field :

A number field with signature :

Scope  (4)

Radical expressions:

Root objects:

AlgebraicNumber objects:

NumberFieldSignature threads automatically over lists:

Applications  (1)

Signatures of Galois extension fields of are of the form or for some integer :

The number field is not a Galois extension of :

Properties & Relations  (3)

The minimal polynomial of has two real roots and a pair of complex roots:

The signature of the number field generated by :

The degree of a number field:

Use Exponent and MinimalPolynomial to verify the result:

Find the signature of the number field :

Wolfram Research (2007), NumberFieldSignature, Wolfram Language function, https://reference.wolfram.com/language/ref/NumberFieldSignature.html.

Text

Wolfram Research (2007), NumberFieldSignature, Wolfram Language function, https://reference.wolfram.com/language/ref/NumberFieldSignature.html.

CMS

Wolfram Language. 2007. "NumberFieldSignature." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NumberFieldSignature.html.

APA

Wolfram Language. (2007). NumberFieldSignature. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NumberFieldSignature.html

BibTeX

@misc{reference.wolfram_2025_numberfieldsignature, author="Wolfram Research", title="{NumberFieldSignature}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/NumberFieldSignature.html}", note=[Accessed: 30-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_numberfieldsignature, organization={Wolfram Research}, title={NumberFieldSignature}, year={2007}, url={https://reference.wolfram.com/language/ref/NumberFieldSignature.html}, note=[Accessed: 30-July-2025 ]}