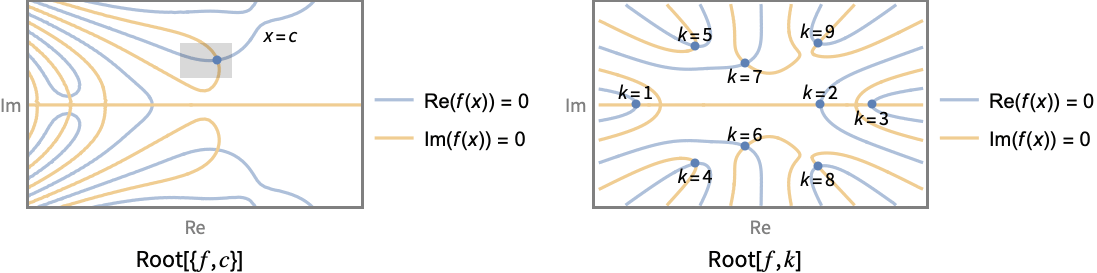
Root

Root[{f,c}]

represents the exact root of the general equation f[x]0 near x=c.

Root[{{f1,…,fn},{c1,…,cn}},j]

represents the j^(th) coordinate of the exact root of the system of equations {f1[x1,…,xn]0,…,fn[x1,…,xn]0} near {x1,…,xn}={c1,…,cn}.

Root[f,k]

represents the exact k^(th) root of the polynomial equation f[x]0.

Root[{f1,f2,…},{k1,k2,…}]

represents the last coordinate of the exact vector {a1,a2,…} such that ai is the ki^(th) root of the polynomial equation fi[a1,…,ai-1,x]0.

Details and Options

  • Root is also known as an algebraic number when f is polynomial with integer coefficients or a transcendental number when there is no such polynomial f possible.
  • Root is typically used to represent an exact number and is automatically generated by a variety of algebra, calculus, optimization and geometry functions.
  • Root represents an exact number as a solution to an equation f[x]0 with additional information specifying which of the roots is intended.
  • Root numbers can be used like any other numbers, both in exact and approximate computations.
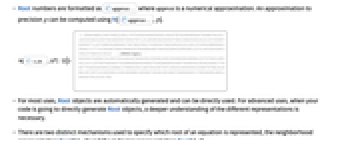
  • Root numbers are formatted as where approx is a numerical approximation. An approximation to precision p can be computed using N[,p].
  • For most uses, Root objects are automatically generated and can be directly used. For advanced uses, when your code is going to directly generate Root objects, a deeper understanding of the different representations is necessary.
  • There are two distinct mechanisms used to specify which root of an equation is represented, the neighborhood representation Root[{f,c}] and the indexing representation Root[f,k].
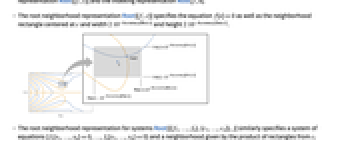
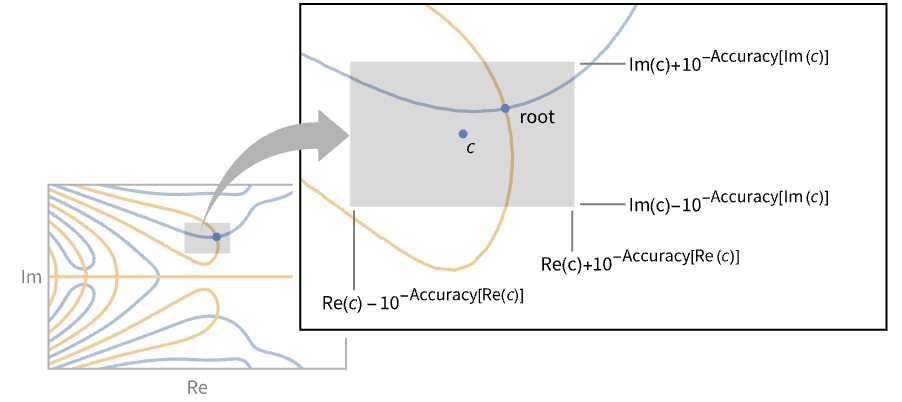
  • The root neighborhood representation Root[{f,c}] specifies the equation f[x]0 as well as the neighborhood rectangle centered at c and width 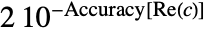and height .
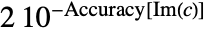  • The root neighborhood representation for systems Root[{{f1,…,fn},{c1,…,cn}},j] similarly specifies a system of equations {f1[x1,…,xn]0,…,fn[x1,…,xn]0} and a neighborhood given by the product of rectangles from ci for the different coordinates.
  • The root neighborhood representation Root[{f,c,m}] specifies that f[x]0 has a root of multiplicity m in the neighborhood given by c. However, it may be a cluster of closely spaced roots and by refining the neighborhood c, i.e. higher precision root approximation, they may separate. »
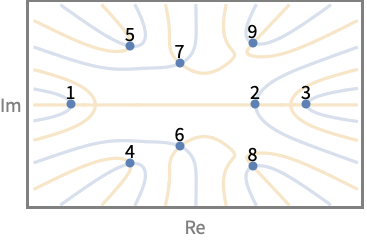
  • The root indexing representation Root[f,k] applies to polynomial functions f only. The indexing of roots takes the real roots first, in increasing order. For polynomials with rational coefficients, the complex conjugate pairs of roots have consecutive indices.
  • The root indexing representation for systems Root[{f1,f2,…,fk},{k1,k2,…,kn}] applies to triangular systems of polynomial equations only. Given equations f1[x1]0, f2[x1,x2]0, …, fn[x1,x2,…,xn]0, we recursively define r1 as the k1^(th) root of f1[x1]0, r2 as the k2^(th) root of f2[r1,x2]0 and finally rn as the kn^(th) root of fn[r1,…,rn-1,xn]0. The represented root is rn.

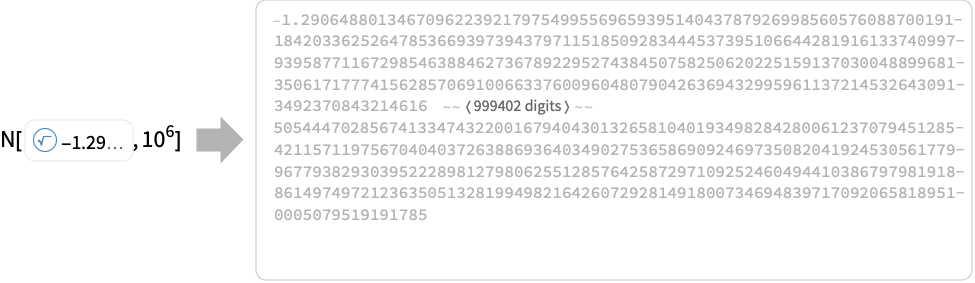
Examples

open allclose all

Basic Examples  (4)

Solution to a quintic:

Numerical values:

Real solutions to an exp-log equation:

Real solution to a system of equations:

A solution instance to a system of transcendental equations:

Scope  (22)

Basic Uses  (5)

Some exact values are generated automatically:

Evaluate to high precision:

Exact comparisons:

Convert radicals to a Root object:

Convert a Root object to radicals:

Disable the elided formatting of Root:

Re-enable the elided formatting:

Roots of Univariate Functions  (4)

Real roots of an exp-log function:

The Root representation involves a univariate function and an approximation that isolates the root:

The Root object is an exact numeric expression:

Roots of an analytic function in a bounded region:

A triple root:

This representation is used for roots of polynomials of degrees that exceed $MaxRootDegree:

The approximation used to represent the root is equal to , but the root is not:

Roots of Multivariate Systems  (1)

Find a solution instance to a system of transcendental equations:

The roots are exact numeric expressions:

The Root representation involves a multivariate system and an approximation that isolates the root:

Roots of Univariate Polynomials  (10)

Roots of a univariate polynomial with rational coefficients are algebraic numbers:

The polynomials are automatically reduced:

A minimal polynomial is always irreducible and primitive:

Use MinimalPolynomial to extract the minimal polynomial:

A Root object representing an algebraic number has three arguments:

The third argument is 0 (default value) or 1 and indicates the root isolation method to be used:

The root isolation method used may affect the ordering of non-real roots:

Roots of polynomials of degree at 1 and 2 simplify automatically:

An algebraic combination of algebraic numbers is an algebraic number:

Use RootReduce to represent the result as a single Root object:

The canonicalization is not done automatically since minimal polynomials can grow rapidly:

Complex components of algebraic numbers:

Root of a polynomial with exact numeric coefficients is an exact numeric object:

Roots of a polynomial with coefficients involving symbolic parameters:

Plot the real-valued roots:

Find the series with respect to the parameter:

Find Puiseux series of a root at a branch point:

Roots of a quadratic with symbolic coefficients:

When a, b, c and the roots are real, the roots are always ordered by their values:

The "standard" formulas for the roots of a quadratic do not guarantee the ordering of roots:

Roots of Triangular Polynomial Systems  (2)

Real root of a triangular system of equations:

The Root representation involves a triangular polynomial system and root indices:

The Root object is an exact numeric expression:

Roots of systems of polynomials with rational coefficients have algebraic number coordinates:

The degree of the minimal polynomial is generally the product of degrees of the system polynomials:

This representation is used for roots of polynomials with algebraic number coefficients:

Convert the root to the canonical algebraic number representation:

Options  (1)

ExactRootIsolation  (1)

Root[f,k] by default isolates the complex roots of a polynomial using validated numerical methods. Setting ExactRootIsolationTrue will make Root use symbolic methods that are usually much slower.

The setting of ExactRootIsolation is reflected in the third argument of a Root object:

Root isolation is performed the first time the numerical value of the root is needed:

The symbolic complex root isolation method is usually slower than the validated numeric one:

The root isolation method may affect the ordering of nonreal roots:

Applications  (19)

Solve polynomial equations of any degree in closed form in terms of Root:

Solve the characteristic equation of a Hilbert matrix:

Using Eigenvalues:

Find the minimum of a parameterized polynomial:

Solve a constant coefficient differential equation of any degree:

Solve a constant coefficient difference equation of any degree:

Find a solution of a triangular system of equations:

Represent the solution in the Root[f,k] form:

Here, the Root[f,k] representation would involve a polynomial of degree 1000000:

Compute an approximate value of the solution:

Resolve a piecewise function:

Solve univariate exp-log equations and inequalities over the reals:

Solve univariate elementary function equations over bounded intervals and regions:

Solve univariate analytic equations over bounded intervals and regions:

Find real roots of high-degree sparse polynomials and algebraic functions:

Solve univariate transcendental optimization problems:

Integrate a piecewise function with an exp-log inequality condition:

Evaluate the hard hexagon entropy constant:

Solve Kepler's equation:

Compute the Laplace limit constant:

Plot a root as a function of a parameter:

Solve a convex optimization problem:

Find a solution instance of a system of transcendental equations and inequalities:

Properties & Relations  (11)

Root objects represent exact numbers:

Compute approximations to arbitrary precision:

Use MinimalPolynomial to find minimal polynomials of algebraic numbers:

Use ToRadicals to attempt to convert a Root object to an arithmetic combination of radicals:

All roots of polynomials of degree not exceeding 4 are representable in radicals:

Use RootReduce to canonicalize algebraic numbers, including from operations:

From a triangular system:

Use AlgebraicNumber for computations within a fixed simple extension of the rationals:

Rational operations on AlgebraicNumber objects produce AlgebraicNumber objects:

Use ToNumberField to express given algebraic numbers as elements of the same simple extension:

Perform computations within the common simple extension or rationals:

RootSum represents the sum of values of a function over roots of a polynomial:

Use Normal to represent the sum using explicit roots:

For rational functions, the sum can be computed without finding the roots:

Simplify combinations of Root objects:

Solve an equation for a parameter in a Root object:

Use ImplicitD to compute derivatives of implicit solutions of equations:

Compare with the result obtained by computing the derivative of directly:

Compute series expansions of implicit solutions to equations:

Use AsymptoticSolve to find series expansions of all roots:

Use RootApproximant to generate Root objects that approximate given numbers:

Possible Issues  (5)

Series at branch points may not be valid in all directions:

Canonicalization is only possible for parameter‐free roots:

Parameterized roots can have complicated branch cuts in the complex parameter plane:

A non-polynomial Root object may represent a cluster of distinct roots:

Numerical computation with a higher precision yields an approximation of one of the roots:

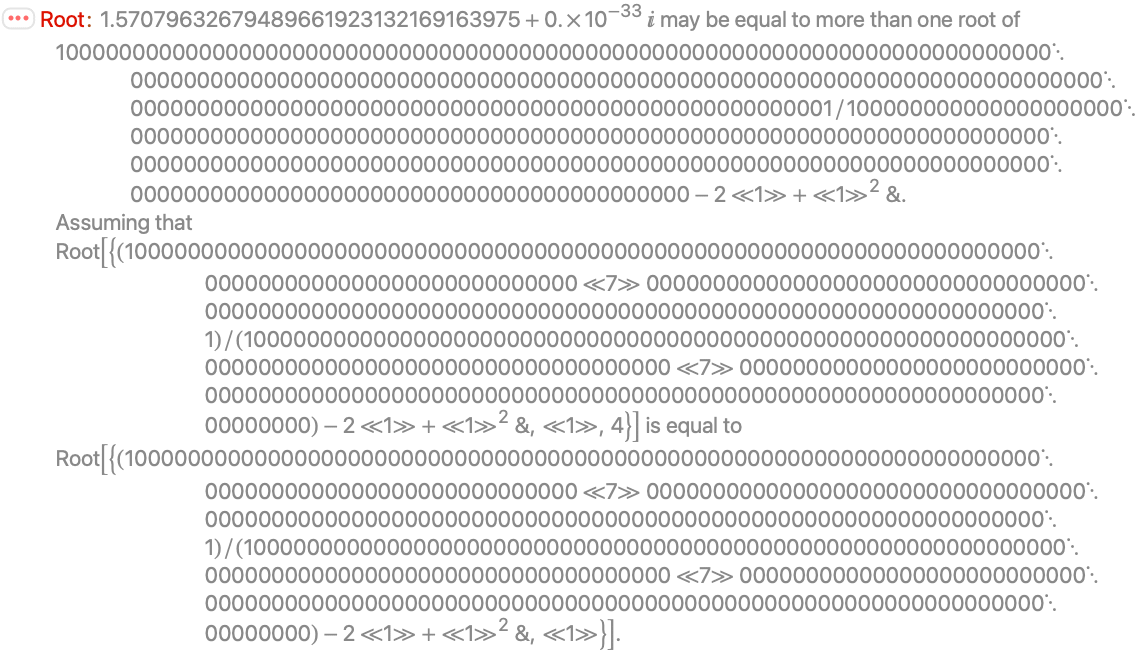
The choice of root stays the same for subsequent computations:

A larger setting for $MaxExtraPrecision can be needed for roots with noninteger coefficients:

Neat Examples  (1)

A high power of a Pisot number that is nearly an integer:

Wolfram Research (1996), Root, Wolfram Language function, https://reference.wolfram.com/language/ref/Root.html (updated 2021).

Text

Wolfram Research (1996), Root, Wolfram Language function, https://reference.wolfram.com/language/ref/Root.html (updated 2021).

CMS

Wolfram Language. 1996. "Root." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Root.html.

APA

Wolfram Language. (1996). Root. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Root.html

BibTeX

@misc{reference.wolfram_2022_root, author="Wolfram Research", title="{Root}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Root.html}", note=[Accessed: 30-June-2022 ]}

BibLaTeX

@online{reference.wolfram_2022_root, organization={Wolfram Research}, title={Root}, year={2021}, url={https://reference.wolfram.com/language/ref/Root.html}, note=[Accessed: 30-June-2022 ]}