WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

ObservableDecomposition[sys]

系 sys の可観測な部分系を与える

ObservableDecomposition[sys,{z1,…}]

新しい座標 ziを指定する．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
アプリケーション  
線形系  
Affine Systems  
特性と関係  
関連項目
関連するガイド
履歴
引用書式

ObservableDecomposition

ObservableDecomposition[sys]

系 sys の可観測な部分系を与える

ObservableDecomposition[sys,{z1,…}]

新しい座標 ziを指定する．

詳細とオプション

例題

すべて開く すべて閉じる

例  (1)

可観測部分系とその変換を求める：

Wolfram Language code: ObservableDecomposition[StateSpaceModel[{{{Subscript[a, 1], 0, 0}, {0, Subscript[a, 2], 0}, {0, 0, Subscript[a, 3]}}, {{Subscript[b, 1]}, {Subscript[b, 2]}, {Subscript[b, 3]}}, {{Subscript[c, 1], 0, Subscript[c, 3]}}, {{Subscript[d, 11]}}}, SamplingPeriod -> None, SystemsModelLabels -> None]]

スコープ  (4)

可観測系の可観測部分系は完全な系である：

Wolfram Language code: ssm = StateSpaceModel[{{{0, 0, -2}, {1, 0, -3}, {0, 1, -1}}, {{3}, {-2}, {1}}, {{0, 0, 1}}, {{0}}}, SamplingPeriod -> None, SystemsModelLabels -> None]; ObservableDecomposition[ssm]

部分的に可観測な連続時間系の可観測部分系：

Wolfram Language code: ssm = StateSpaceModel[{{{3, 6, 4}, {9, 6, 10}, {-7, -7, -9}}, {{1/3, 2/3}, {2/3, 1/3}, {-1/6, 1/3}}, {{1, 2, 3}, {3, 3, 6}}, {{0, 0}, {0, 0}}}, SamplingPeriod -> None, SystemsModelLabels -> None];
Wolfram Language code: MatrixForm /@ ObservableDecomposition[N@ssm]

ディスクリプタ系の可観測部分系：

Wolfram Language code: ObservableDecomposition[StateSpaceModel[{{{Subscript[a, 1], 0, 0}, {0, Subscript[a, 2], 0}, {0, 0, Subscript[a, 3]}}, {{0, 0}, {Subscript[b, 1], 0}, {0, Subscript[b, 2]}}, {{0, Subscript[c, 1], 0}, {0, 0, Subscript[c, 3]}}, {{Subscript[d, 11], Subscript[d, 12]}, {Subscript[d, 21], Subscript[d, 22]}}, {{Subscript[e, 1], 0, 0}, {0, Subscript[e, 2], 0}, {0, 0, 0}}}, SamplingPeriod -> None, SystemsModelLabels -> None]]

アフィン系の可観測部分系：

Wolfram Language code: ObservableDecomposition[AffineStateSpaceModel[{{-Subscript[x, 2], Subscript[x, 1]* Subscript[x, 2], Subscript[x, 3]}, {{1 + Subscript[x, 2]}, {0}, {0}}, {Subscript[x, 1]}, {{0}}}, {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3]}, {Subscript[, 1]}, {Automatic}, Automatic, SamplingPeriod -> None]]

新たな変数を指定する：

Wolfram Language code: ObservableDecomposition[AffineStateSpaceModel[{{-Subscript[x, 2], Subscript[x, 1]* Subscript[x, 2], Subscript[x, 3]}, {{1 + Subscript[x, 2]}, {0}, {0}}, {Subscript[x, 1]}, {{0}}}, {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3]}, {Subscript[, 1]}, {Automatic}, Automatic, SamplingPeriod -> None], {Subscript[z, 1], Subscript[z, 2], Subscript[z, 3]}]

アプリケーション  (7)

線形系  (4)

Kalman可観測分解を構築する：

Wolfram Language code: ssm = StateSpaceModel[{{{Subscript[a, 1], 0, 0}, {0, Subscript[a, 2], 0}, {0, 0, Subscript[a, 3]}}, {{0, 0}, {Subscript[b, 1], 0}, {0, Subscript[b, 2]}}, {{Subscript[c, 1], 0, 0}, {0, 0, Subscript[c, 3]}}, {{Subscript[d, 11], Subscript[d, 12]}, {Subscript[d, 21], Subscript[d, 22]}}}, SamplingPeriod -> None, SystemsModelLabels -> None];

ObservableDecompositionは，可観測部分系のみを取り出す：

Wolfram Language code: {p, ossm} = ObservableDecomposition[ssm];
Wolfram Language code: ossm

Kalman可観測分解は可観測部分系を最初に置き，残りはそのままにする：

Wolfram Language code: po = NullSpace[p]; (* Orthogonal space *) StateSpaceTransform[ssm, ArrayFlatten[{{p, po}}]]

可観測部分空間の次元を計算する：

Wolfram Language code: {p, ossm} = ObservableDecomposition[StateSpaceModel[{{{Subscript[a, 1], 0, 0}, {0, Subscript[a, 2], 0}, {0, 0, Subscript[a, 3]}}, {{0, 0}, {Subscript[b, 1], 0}, {0, Subscript[b, 2]}}, {{Subscript[c, 1], 0, 0}, {0, 0, Subscript[c, 3]}}, {{Subscript[d, 11], Subscript[d, 12]}, {Subscript[d, 21], Subscript[d, 22]}}}, SamplingPeriod -> None, SystemsModelLabels -> None]];

可観測部分空間は p の範囲である．つまり，列次元である：

Wolfram Language code: Dimensions[p]//Last

以下の系の可観測部分空間を求め，どの状態軌道が出力のみを観測した場合から見分けられるかを示す：

Wolfram Language code: ssm = StateSpaceModel[{{{-6, -2, -3}, {3, -1, 3}, {2, 2, -1}}, {{1}, {0}, {-2}}, {{0, 1, -1}}, {{0}}}, SamplingPeriod -> None, SystemsModelLabels -> None];

系は非可観測であり，出力からの部分空間のみが可観測である：

Wolfram Language code: ObservableModelQ[ssm]

変換 p の範囲は可観測部分空間を与える：

Wolfram Language code: {p, osys} = ObservableDecomposition[ssm];
Wolfram Language code: ospace = ParametricPlot3D[p.{u, v}, {u, -1, 1}, {v, -1, 1}, Mesh -> None, PlotStyle -> Opacity[0.7]]

初期値が可観測部分空間の1点に投影している軌道のシミュレーションを行う：

Wolfram Language code: w = First@NullSpace[p]; x0 = Table[p.{0.5, 0.5} + λ w, {λ, -0.4, 0.4, 0.2}]; sr = Table[StateResponse[{ssm, x}, Sin[2t], {t, 0, 10}], {x, x0}];
Wolfram Language code: Show[ParametricPlot3D[Evaluate[sr], {t, 0, 10}], ospace, ParametricPlot3D[Evaluate[p.{0.5, 0.5} + λ w], {λ, -0.5, 0.5}]]

出力を観測すると，これらの軌道がすべて等しく見える：

Wolfram Language code: or = Table[OutputResponse[{ssm, x}, Sin[2t], {t, 0, 10}], {x, x0}];
Wolfram Language code: Plot[or, {t, 0, 10}]

使用可能な測度を使って状態を決定し，推定器を設計する：

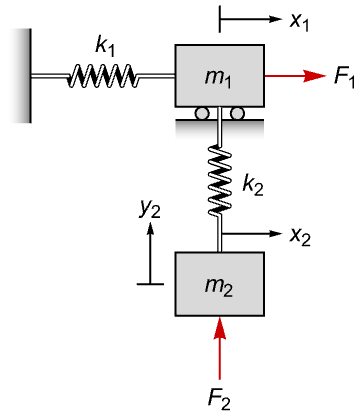
質量 の位置のみが測定されるので，この系は完全に可観測な訳ではない：

Wolfram Language code: pars = {Subscript[k, 1] -> 75, Subscript[k, 2] -> 100, Subscript[m, 1] -> 1, Subscript[m, 2] -> 0.5};
Wolfram Language code: ssm = StateSpaceModel[{{{0, 1, 0, 0, 0, 0}, {-(Subscript[k, 1] + Subscript[k, 2])/Subscript[m, 1], 0, Subscript[k, 2]/Subscript[m, 1], 0, 0, 0}, {0, 0, 0, 1, 0, 0}, {Subscript[k, 2]/Subscript[m, 2], 0, -Subscript[k, 2]/Subscript[m, 2], 0, 0, 0}, {0, 0, 0, 0, 0, 1}, {0, 0, 0, 0, -Subscript[k, 2]/Subscript[m, 2], 0}}, {{0, 0}, {Subscript[m, 1]^(-1), 0}, {0, 0}, {0, 0}, {0, 0}, {0, Subscript[m, 2]^(-1)}}, {{1, 0, 0, 0, 0, 0}}, {{0, 0}}}, SamplingPeriod -> None, SystemsModelLabels -> {None, None, {Subscript[x, 1], Subscript[v, 1], Subscript[x, 2], Subscript[v, 2*x], Subscript[y, 2], Subscript[v, 2*y]}}] /. pars;
Wolfram Language code: ObservableModelQ[ssm]

変換行列 の0の行に関連する状態は，観測することができない：

Wolfram Language code: {p, osys} = ObservableDecomposition[ssm];
Wolfram Language code: Position[p, {_ ? PossibleZeroQ..}]

推定器を設計し，最初の4状態の任意の組合せを推定することができる：

Wolfram Language code: ℓ = EstimatorGains[osys, {-1, -2, -3 + I, -3 - I}]

を推定する推定器：

Wolfram Language code: StateOutputEstimator[osys, ℓ];
Wolfram Language code: est = SystemsModelSeriesConnect[%, TransferFunctionModel[{PadRight[p[[3]], 5]}]]

入力信号集合と初期条件に対する の応答を計算する：

Wolfram Language code: inps = {UnitStep[t] - UnitStep[t - 2], UnitStep[t - 1] - UnitStep[t - 3]}; ics = {0.01, 0, 0.1, 0, 0.05, 0};
Wolfram Language code: x2 = StateResponse[{ssm, ics}, inps, {t, 0, 8}][[3]]; Plot[x2, {t, 0, 8}]

推定された状態オブジェクト：

Wolfram Language code: x2e = OutputResponse[est, Join[inps, OutputResponse[{ssm, ics}, inps, {t, 0, 8}]], {t, 0, 8}];
Wolfram Language code: Plot[{x2, x2e}, {t, 0, 8}, PlotLegends -> {"actual", "estimated"}, PlotRange -> All]

Affine Systems  (3)

三角形可観測分解を構築する：

Wolfram Language code: assm = AffineStateSpaceModel[{{Subscript[x, 1], -Subscript[x, 1] + Subscript[x, 2] + Subscript[x, 1]*Subscript[x, 2], -Subscript[x, 1] - Subscript[x, 3]}, {{0}, {1}, {1 + Subscript[x, 1]}}, {Subscript[x, 2]}, {{0}}}, {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3]}, Automatic, {Automatic}, Automatic, SamplingPeriod -> None];

ObservableDecompositionは，可観測な部分系のみを取り出す：

Wolfram Language code: {{p1, p2}, osys} = ObservableDecomposition[assm];
Wolfram Language code: osys

三角形か観測分解は可観測な部分系を最初に置き，残りをそのままに保つ：

Wolfram Language code: StateSpaceTransform[assm, {p1, Flatten[p2]}]

可観測部分空間の次元を計算する：

Wolfram Language code: assm = AffineStateSpaceModel[{{E^Subscript[x, 2]*Subscript[x, 2] + Subscript[x, 1]*Subscript[x, 3], Subscript[x, 3], (-Subscript[x, 2])*Subscript[x, 3] + Subscript[x, 4], (-Subscript[x, 2]^2)*Subscript[x, 3] + Subscript[x, 3]^2 + Subscript[x, 2]*Subscript[x, 4]}, {{Subscript[x, 1]}, {1}, {0}, {Subscript[x, 3]}}, {Subscript[x, 3]}, {{0}}}, {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3], Subscript[x, 4]}, Automatic, {Automatic}, Automatic, SamplingPeriod -> None];
Wolfram Language code: ObservableModelQ[assm]

次元は逆変換 から得ることができる：

Wolfram Language code: {{Subscript[p, 1], Subscript[p, 2]}, ossm} = ObservableDecomposition[assm];
Wolfram Language code: ossm
Wolfram Language code: Length[First[Subscript[p, 2]]]

出力の区別がつかない部分空間を求める：

Wolfram Language code: asys = AffineStateSpaceModel[{{E^Subscript[x, 2]*Subscript[x, 2] + Subscript[x, 1]*Subscript[x, 3], Subscript[x, 3], (-Subscript[x, 2])*Subscript[x, 3] + Subscript[x, 4], (-Subscript[x, 2]^2)*Subscript[x, 3] + Subscript[x, 3]^2 + Subscript[x, 2]*Subscript[x, 4]}, {{Subscript[x, 1]}, {1}, {0}, {Subscript[x, 3]}}, {Subscript[x, 3]}, {{0}}}, {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3], Subscript[x, 4]}, Automatic, {Automatic}, Automatic, SamplingPeriod -> None];

この系は観測できない．ゆえに，部分空間のみが出力から可観測である：

Wolfram Language code: ObservableModelQ[asys]

区別がつかない部分空間：

Wolfram Language code: {{Subscript[p, 1], {Subscript[p, 21], Subscript[p, 22]}}, osys} = ObservableDecomposition[asys];
Wolfram Language code: isubspace[{x1_, x2_, x3_, x4_}] := Last /@ Subscript[p, 21] /. {Subscript[x, 1] -> x1, Subscript[x, 2] -> x2, Subscript[x, 3] -> x3, Subscript[x, 4] -> x4}
Wolfram Language code: isubspace[{Subscript[x, 1], Subscript[x, 2], Subscript[x, 3], Subscript[x, 4]}]

部分空間上の2点：

Wolfram Language code: Subscript[pt, 1] = {1, 3, 1, 2}; Subscript[pt, 2] = {1, 1, 1, 0};
Wolfram Language code: isubspace /@ {Subscript[pt, 1], Subscript[pt, 2]}

2点からの出力の軌跡は等しい：

Wolfram Language code: Table[OutputResponse[{asys, pt}, UnitStep[t], {t, 0, 1}], {pt, {Subscript[pt, 1], Subscript[pt, 2]}}];
Wolfram Language code: Table[Plot[or, {t, 0, 1}], {or, Flatten[%, 1]}]

特性と関係  (2)

変換行列 p は，StateSpaceTransformを使って可観測部分系を選ぶ：

Wolfram Language code: ssm = StateSpaceModel[{{{Subscript[a, 1], 0, 0}, {0, Subscript[a, 2], 0}, {0, 0, Subscript[a, 3]}}, {{0, 0}, {Subscript[b, 1], 0}, {0, Subscript[b, 2]}}, {{Subscript[c, 1], 0, 0}, {0, 0, Subscript[c, 3]}}, {{Subscript[d, 11], Subscript[d, 12]}, {Subscript[d, 21], Subscript[d, 22]}}}, SamplingPeriod -> None, SystemsModelLabels -> None];
Wolfram Language code: {p, osys} = ObservableDecomposition[ssm]; tsys = StateSpaceTransform[ssm, {p, p}];
Wolfram Language code: {osys, tsys}

アフィン系については，変換規則が可観測系を選ぶ：

Wolfram Language code: assm = AffineStateSpaceModel[{{-Subscript[x, 4], 0, -Subscript[x, 1], Subscript[x, 2]}, {{1}, {0}, {1 + Subscript[x, 2]}, {0}}, {Subscript[x, 1], Subscript[x, 2]}, {{0}, {0}}}, {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3], Subscript[x, 4]}, {Subscript[, 1]}, {Automatic, Automatic}, Automatic, SamplingPeriod -> None];
Wolfram Language code: {p, osys} = ObservableDecomposition[assm]; tsys = StateSpaceTransform[assm, p];
Wolfram Language code: {osys, tsys}
Wolfram Research (2010), ObservableDecomposition, Wolfram言語関数， https://reference.wolfram.com/language/ref/ObservableDecomposition.html （2014年に更新）.

テキスト

Wolfram Research (2010), ObservableDecomposition, Wolfram言語関数， https://reference.wolfram.com/language/ref/ObservableDecomposition.html （2014年に更新）.

CMS

Wolfram Language. 2010. "ObservableDecomposition." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ObservableDecomposition.html.

APA

Wolfram Language. (2010). ObservableDecomposition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ObservableDecomposition.html

BibTeX

@misc{reference.wolfram_2026_observabledecomposition, author="Wolfram Research", title="{ObservableDecomposition}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ObservableDecomposition.html}", note=[Accessed: 04-August-2026]}

BibLaTeX

@online{reference.wolfram_2026_observabledecomposition, organization={Wolfram Research}, title={ObservableDecomposition}, year={2014}, url={https://reference.wolfram.com/language/ref/ObservableDecomposition.html}, note=[Accessed: 04-August-2026]}