StateSpaceTransform

StateSpaceTransform[sys,{p,q}]

transforms the state-space model sys using the matrices p and q.

StateSpaceTransform[sys,{{x1p1[z],…},{z1q1[x],…}}]

transforms using the variable transformations {x1p1[z],…} and {z1q1[x],…}.

Details and Options

  • StateSpaceTransform returns a transformed model where the state variables have been transformed. The transformation can be a similarity, equivalence, or restricted equivalence transformation.
  • The system sys can be a standard or descriptor StateSpaceModel, AffineStateSpaceModel, or NonlinearStateSpaceModel.
  • For a standard StateSpaceModel[{a,b,c,d}], the original and transformed systems are related by the transformation 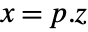and the corresponding equations are given by:
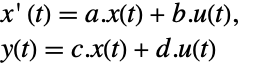
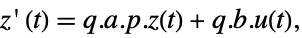
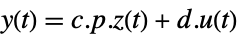
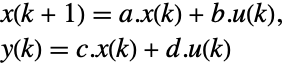
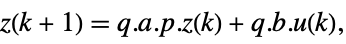
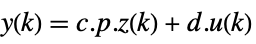
  • Typically p and q are inverses, in which case the transformation is a similarity transformation. The following defaults for p and q are used for standard StateSpaceModel transformations:
  • p or {p,Automatic}{p,Inverse[p]}
    {Automatic,q}{Inverse[q],q}
  • For a descriptor StateSpaceModel[{a,b,c,d,e}], the original and transformed systems related by the transformation 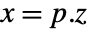and the corresponding equations are given by:
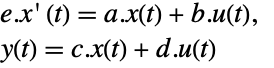
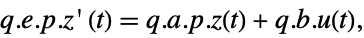
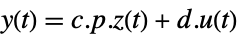
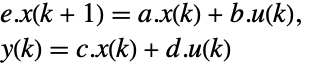
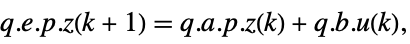
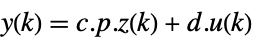
  • Typically p and q are invertible matrices but not inverses, in which case the transformation is an equivalence transformation. The following defaults are used for descriptor StateSpaceModel transformations:
  • p or {p,Automatic}{p,IdentityMatrix[n]}
    {Automatic,q}{IdentityMatrix[n],q}
  • For an AffineStateSpaceModel[{a,b,c,d},x] and NonlinearStateSpaceModel[{f,g},x,u] with j the Jacobian matrix D[p[z],{z}], the original and transformed systems are related by the transformation 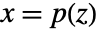, and the corresponding equations are given by:
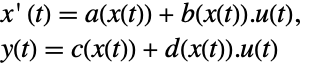
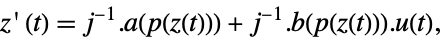
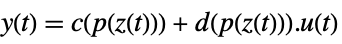
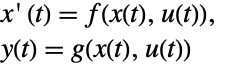
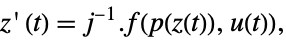
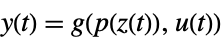
  • Typically p[z] and q[x] are inverses, in which case the transformation is an invertible mapping.
  • {{x1->p1[z],…},{z1,…}}q[x] is computed if needed
    {Automatic,{z1->q[x],…}}p[z] is computed
  • When variable transformation matrices {p,q} are given, the resulting system is of the same type as the input. In the case of nonlinear state-space models, these are taken to represent the transformation rules {{x1->p〚1〛.z,…},{z1->q〚1〛.x,…}}.
  • When variable transformation rules {{x1->p1[z],…},…} are given, the resulting system is always AffineStateSpaceModel or NonlinearStateSpaceModel.
  • StateSpaceTransform accepts the option DescriptorStateSpace.

Examples

open allclose all

Basic Examples  (1)

A similarity transformation :

Use the matrix pair:

Scope  (15)

Linear Transformations  (10)

The similarity transformation :

Specify the matrix pair:

Specify the transformation as :

The similarity transform for a descriptor system:

The equivalence transform for a descriptor system:

The corresponding matrix pair specification:

Obtain an equivalent descriptor system with the state equations premultiplied by a matrix q:

The new states are essentially the old states, i.e. :

For a descriptor system, the transformation with an invertible p and q gives an equivalent system:

The original system:

A noninvertible p or q gives a system with restricted equivalence:

Linear discrete-time systems behave just like continuous-time systems under matrix transformations:

Transform an AffineStateSpaceModel according to :

Specify the transformation in terms of the new variable z:

Specify the transformation as :

Using variables:

Specify the transformation and its inverse:

Transform a NonlinearStateSpaceModel according to :

In terms of the new variable z:

In terms of the inverse transformation:

The transformation and its inverse:

For orthogonal matrices, Transpose can be used instead of Automatic or Inverse:

Nonlinear Transformations:  (5)

Nonlinear transformations of a StateSpaceModel:

Nonlinear transformations of an AffineStateSpaceModel:

Nonlinear transformations of a NonlinearStateSpaceModel:

Specify a nonlinear transformation and its inverse:

The inverse of a nonlinear transformation is required only if operating points are specified:

Generalizations & Extensions  (2)

A non-square orthogonal matrix selects a subsystem:

The corresponding matrix pair:

For nonlinear transformations, a partitioned inverse specification selects a subsystem:

The complete system:

Options  (1)

DescriptorStateSpace  (1)

Treat a standard StateSpaceModel as a descriptor system:

It gives the same result as an explicit descriptor specification:

Similar results can be obtained with the inverse transformation as well:

Applications  (6)

A function to obtain the controllable companion form of a single-input system:

A function to obtain the observable companion form of a single-output system:

Rearrange the states:

Convert the model of a simple pendulum in Cartesian coordinates to polar coordinates:

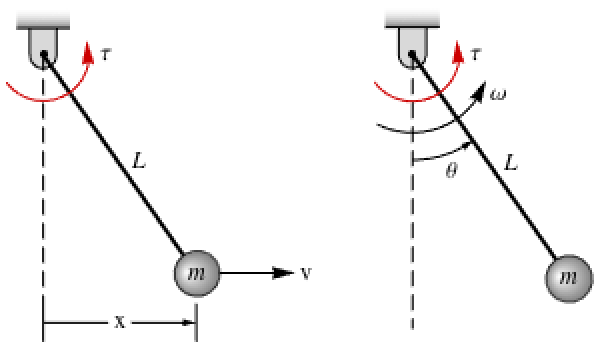
The model in Cartesian coordinates:

The model in polar coordinates:

Apply a direct quadrature (dq) transformation to a permanent magnet stepper motor model: »

Apply the dq transformation to the currents and :

Apply the dq transformation to the input voltages as well:

Convert aircraft equations of motion from body to wind coordinates:

Properties & Relations  (8)

The output response is invariant under a similarity transformation:

Similar systems have identical transfer functions:

The eigenvalues (and hence, stability) are invariant under a similarity transformation:

Controllability and observability are invariant under a similarity transformation:

The Hankel singular values are invariant under similarity transformation:

Systems model decompositions all use state transformations:

ControllableDecomposition based on ControllabilityMatrix:

ObservableDecomposition based on ObservabilityMatrix:

InternallyBalancedDecomposition based on ObservabilityGramian:

JordanModelDecomposition based on JordanDecomposition:

KroneckerModelDecomposition:

The linearization using coordinate transformations is also related using StateSpaceTransform:

A state transformation is an intermediate step in feedback linearization:

Apply the feedback and then the state transformation to get the transformed system:

The property "TransformedSystem" gives the same result:

Possible Issues  (2)

The transformation matrix must be orthonormal or invertible:

It is neither orthonormal nor invertible:

If there are multiple inverse solutions, only one is chosen:

There are 3 inverse solutions:

Choose a desired inverse:

Wolfram Research (2010), StateSpaceTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/StateSpaceTransform.html (updated 2014).

Text

Wolfram Research (2010), StateSpaceTransform, Wolfram Language function, https://reference.wolfram.com/language/ref/StateSpaceTransform.html (updated 2014).

CMS

Wolfram Language. 2010. "StateSpaceTransform." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/StateSpaceTransform.html.

APA

Wolfram Language. (2010). StateSpaceTransform. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StateSpaceTransform.html

BibTeX

@misc{reference.wolfram_2024_statespacetransform, author="Wolfram Research", title="{StateSpaceTransform}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/StateSpaceTransform.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_statespacetransform, organization={Wolfram Research}, title={StateSpaceTransform}, year={2014}, url={https://reference.wolfram.com/language/ref/StateSpaceTransform.html}, note=[Accessed: 22-November-2024 ]}