OrderedQ

OrderedQ[h[e1,e2,…]]

ei が正規順序に並ぶ場合にはTrueを，その他の場合にはFalseを与える．

OrderedQ[h[e1,e2,…],p]

順序関数 p を使って要素 ei, ei+1の各ペアが順に並んでいるかどうかを判定する．

詳細

  • OrderedQ[{e,e}]は，Trueを与える．
  • デフォルトで，OrderedQ[list,p]はSortの説明に記されているように正規順序を使う．これは，Orderを順序関数 p として指定することと同じである． »
  • 要素ペア e1, e2に適用された順序関数 p は，1，0または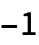-1あるいはTrueまたはFalseを返す．p[e1,e2]の値は次のように解釈される．
  • 1e1は e2の前
    0e1と e2は同一なものとして扱われなければならない
    -1e1は e2の後ろ
    Truee1と e2は順序通りである
    Falsee1と e2は順序通りではない
  • 順序関数 p が上記以外の値 p[e1,e2]を返すとき，e1と e2は事実上順序付けられているものとして扱われる． »

例題

すべて開くすべて閉じる

例  (4)

数のリストが順序付けられているかどうかをチェックする：

文字列のリストが順序付けられているかどうかをチェックする：

数式がその構造でソートされているかどうかをチェックする：

数値がソートされているかどうかをチェックする：

各要素の第2部分だけを調べる際に，リストが順序付けられているかどうかをチェックする：

スコープ  (8)

OrderedQは任意の式で使うことができる：

OrderedQはListだけでなく，任意の頭部で使うことができる：

連想の値が順序づけられているかどうかをチェックする：

順序関数としてGreaterを指定する：

GreaterEqualを使って要素の繰返しが使えるようにする：

NumericalOrderを使って複素数と数のような式が使えるようにする：

AlphabeticOrderで特定の言語の規則に従ってソートする：

記号を数の前に置くカスタムの順序関数を定義する：

純関数の順序関数を使う：

アプリケーション  (2)

順番になっているタプルを求める：

どのタプルが順番になっているかを見る：

特性と関係  (7)

OrderedQ[expr]はOrderedQ[expr,Order]に等しい：

比較は，ペアが順序通りではないと判定された時点で終了する：

明示的な数については，OrderedQは，事実上，LessEqualに等しい：

任意の連想についてOrderedQ[assoc,…]==OrderedQ[Values[assoc],…]である：

Sort[expr]===expr のとき，OrderedQ[expr]はTrueを与える：

Sortは，デフォルトで，事実上OrderedQを使ってソートする：

OrderedQは，デフォルトで，あまり厳密ではない順序を使う：

UnsameQを順序関数に加えて厳密な標準順序かどうかチェックする：

Orderが1を与えるかどうかを調べることもできる：

考えられる問題  (2)

OrderedQは，数値によってではなく，デフォルトで構造的に作用する：

要素を数値化するか，NumericalOrderを使って数値によって比較するかする：

順序関数で認識できない値の要素は順序付けられていると解釈される：

TrueQを使って，比較できなかったものを順序付けられていないものとして解釈する：

Wolfram Research (1988), OrderedQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/OrderedQ.html （2017年に更新）.

テキスト

Wolfram Research (1988), OrderedQ, Wolfram言語関数， https://reference.wolfram.com/language/ref/OrderedQ.html （2017年に更新）.

CMS

Wolfram Language. 1988. "OrderedQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/OrderedQ.html.

APA

Wolfram Language. (1988). OrderedQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/OrderedQ.html

BibTeX

@misc{reference.wolfram_2024_orderedq, author="Wolfram Research", title="{OrderedQ}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/OrderedQ.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_orderedq, organization={Wolfram Research}, title={OrderedQ}, year={2017}, url={https://reference.wolfram.com/language/ref/OrderedQ.html}, note=[Accessed: 22-November-2024 ]}