Patterns
Patterns
Patterns are used throughout the Wolfram Language to represent classes of expressions. A simple example of a pattern is the expression f[x_]. This pattern represents the class of expressions with the form f[anything].
The main power of patterns comes from the fact that many operations in the Wolfram Language can be done not only with single expressions, but also with patterns that represent whole classes of expressions.
You can use patterns in transformation rules to specify how classes of expressions should be transformed:
The basic object that appears in almost all Wolfram Language patterns is _ (traditionally called "blank" by Wolfram Language programmers). The fundamental rule is simply that _ stands for any expression. On most keyboards the _ underscore character appears as the shifted version of the - dash character.
Thus, for example, the pattern f[_] stands for any expression of the form f[anything]. The pattern f[x_] also stands for any expression of the form f[anything], but gives the name x to the expression anything, allowing you to refer to it on the right‐hand side of a transformation rule.
You can put blanks anywhere in an expression. What you get is a pattern which matches all expressions that can be made by "filling in the blanks" in any way.
| f[n_] |
f
with any argument, named
n
|
| f[n_,m_] | f with two arguments, named n and m |
| x^n_ |
x
to any power, with the power named
n
|
| x_^n_ | any expression to any power |
| a_+b_ | a sum of two expressions |
| {a1_,a2_} | a list of two expressions |
| f[n_,n_] | f with two identical arguments |
One of the most common uses of patterns is for "destructuring" function arguments. If you make a definition for f[list_], then you need to use functions like Part explicitly in order to pick out elements of the list. But if you know for example that the list will always have two elements, then it is usually much more convenient instead to give a definition instead for f[{x_,y_}]. Then you can refer to the elements of the list directly as x and y. In addition, the Wolfram Language will not use the definition you have given unless the argument of f really is of the required form of a list of two expressions.
Here is one way to define a function which takes a list of two elements, and evaluates the first element raised to the power of the second element:
A crucial point to understand is that Wolfram Language patterns represent classes of expressions with a given structure. One pattern will match a particular expression if the structure of the pattern is the same as the structure of the expression, in the sense that by filling in blanks in the pattern you can get the expression. Even though two expressions may be mathematically equal, they cannot be represented by the same Wolfram Language pattern unless they have the same structure.
Thus, for example, the pattern (1+x_)^2 can stand for expressions like (1+a)^2 or (1+b^3)^2 that have the same structure. However, it cannot stand for the expression 1+2a+a^2. Although this expression is mathematically equal to (1+a)^2, it does not have the same structure as the pattern (1+x_)^2.
The fact that patterns in the Wolfram Language specify the structure of expressions is crucial in making it possible to set up transformation rules which change the structure of expressions, while leaving them mathematically equal.
It is worth realizing that in general it would be quite impossible for the Wolfram Language to match patterns by mathematical, rather than structural, equivalence. In the case of expressions like (1+a)^2 and 1+2a+a^2, you can determine equivalence just by using functions like Expand and Factor. But, as discussed in "Reducing Expressions to Their Standard Form" there is no general way to find out whether an arbitrary pair of mathematical expressions are equal.
As another example, the pattern x^_ will match the expression x^2. It will not, however, match the expression 1, even though this could be considered as x^0. "Optional and Default Arguments" discusses how to construct a pattern for which this particular case will match. But you should understand that in all cases pattern matching in the Wolfram Language is fundamentally structural.
The x^n_ matches only x^2 and x^3. 1 and x can mathematically be written as 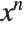 , but do not have the same structure:
, but do not have the same structure:
Another point to realize is that the structure the Wolfram Language uses in pattern matching is the full form of expressions printed by FullForm. Thus, for example, an object such as 1/x, whose full form is Power[x,-1] will be matched by the pattern x_^n_, but not by the pattern x_/y_, whose full form is Times[x_,Power[y_,-1]]. Again, "Optional and Default Arguments" will discuss how you can construct patterns which can match all these cases.
The expressions in the list contain explicit powers of b, so the transformation rule can be applied:
Although the Wolfram Language does not use mathematical equivalences such as  when matching patterns, it does use certain structural equivalences. Thus, for example, the Wolfram Language takes account of properties such as commutativity and associativity in pattern matching.
when matching patterns, it does use certain structural equivalences. Thus, for example, the Wolfram Language takes account of properties such as commutativity and associativity in pattern matching.
To apply this transformation rule, the Wolfram Language makes use of the commutativity and associativity of addition:
The discussion considers only pattern objects such as x_ which can stand for any single expression. Other tutorials discuss the constructs that the Wolfram System uses to extend and restrict the classes of expressions represented by patterns.
| Cases[list,form] | give the elements of list that match form |
| Count[list,form] | give the number of elements in list that match form |
| Position[list,form,{1}] | give the positions of elements in list that match form |
| Select[list,test] | |
| Pick[list,sel,form] | give the elements of list for which the corresponding elements of sel match form |
You can apply functions like Cases not only to lists, but to expressions of any kind. In addition, you can specify the level of parts at which you want to look.
| Cases[expr,lhs->rhs] | find elements of expr that match lhs, and give a list of the results of applying the transformation rule to them |
| Cases[expr,lhs->rhs,lev] | test parts of expr at levels specified by lev |
| Count[expr,form,lev] | give the total number of parts that match form at levels specified by lev |
| Position[expr,form,lev] | give the positions of parts that match form at levels specified by lev |
| Cases[expr,form,lev,n] | find only the first n parts that match form |
| Position[expr,form,lev,n] | give the positions of the first n parts that match form |
The positions are specified in exactly the form used by functions such as Extract and ReplacePart discussed in "Lists":
| DeleteCases[expr,form] | delete elements of expr that match form |
| DeleteCases[expr,form,lev] | delete parts of expr that match form at levels specified by lev |
| ReplaceList[expr,lhs->rhs] | find all ways that expr can match lhs |
Particularly when you use transformation rules, you often need to name pieces of patterns. An object like x_ stands for any expression, but gives the expression the name x. You can then, for example, use this name on the right‐hand side of a transformation rule.
An important point is that when you use x_, the Wolfram Language requires that all occurrences of blanks with the same name x in a particular expression must stand for the same expression.
Thus f[x_,x_] can only stand for expressions in which the two arguments of f are exactly the same. f[_,_], on the other hand, can stand for any expression of the form f[x,y], where x and y need not be the same.
The Wolfram Language allows you to give names not just to single blanks, but to any piece of a pattern. The object x:pattern in general represents a pattern which is assigned the name x. In transformation rules, you can use this mechanism to name exactly those pieces of a pattern that you need to refer to on the right‐hand side of the rule.
| _ | any expression |
| x_ |
any expression, to be named
x
|
| x:pattern | an expression to be named x, matching pattern |
This gives a name to the complete form _^_ so you can refer to it as a whole on the right‐hand side of the transformation rule:
When you give the same name to two pieces of a pattern, you constrain the pattern to match only those expressions in which the corresponding pieces are identical.
You can tell a lot about what "type" of expression something is by looking at its head. Thus, for example, an integer has head Integer, while a list has head List.
In a pattern, _h and x_h represent expressions that are constrained to have head h. Thus, for example, _Integer represents any integer, while _List represents any list.
| x_h | an expression with head h |
| x_Integer | an integer |
| x_Real | an approximate real number |
| x_Complex | a complex number |
| x_List | a list |
| x_Symbol | a symbol |
You can think of making an assignment for f[x_Integer] as like defining a function f that must take an argument of "type" Integer.
The Wolfram Language provides a general mechanism for specifying constraints on patterns. All you need to do is to put /;condition at the end of a pattern to signify that it applies only when the specified condition is True. You can read the operator /; as "slash‐semi", "whenever", or "provided that".
| pattern/;condition | a pattern that matches only when a condition is satisfied |
| lhs:>rhs/;condition | a rule that applies only when a condition is satisfied |
| lhs:=rhs/;condition | a definition that applies only when a condition is satisfied |
You can use /; on whole definitions and transformation rules, as well as on individual patterns. In general, you can put /;condition at the end of any := definition or :> rule to tell the Wolfram Language that the definition or rule applies only when the specified condition holds. Note that /; conditions should not usually be put at the end of = definitions or -> rules, since they will then be evaluated immediately, as discussed in "Immediate and Delayed Definitions".
You can use the /; operator to implement arbitrary mathematical constraints on the applicability of rules. In typical cases, you give patterns which structurally match a wide range of expressions, but then use mathematical constraints to reduce the range of expressions to a much smaller set.
This expression, while mathematically of the correct form, does not have the appropriate structure, so the rule does not apply:
In setting up patterns and transformation rules, there is often a choice of where to put /; conditions. For example, you can put a /; condition on the right‐hand side of a rule in the form lhs:>rhs/;condition, or you can put it on the left‐hand side in the form lhs/;condition->rhs. You may also be able to insert the condition inside the expression lhs. The only constraint is that all the names of patterns that you use in a particular condition must appear in the pattern to which the condition is attached. If this is not the case, then some of the names needed to evaluate the condition may not yet have been "bound" in the pattern‐matching process. If this happens, then the Wolfram Language uses the global values for the corresponding variables, rather than the values determined by pattern matching.
Thus, for example, the condition in f[x_,y_]/;(x+y<2) will use values for x and y that are found by matching f[x_,y_], but the condition in f[x_/;x+y<2,y_] will use the global value for y, rather than the one found by matching the pattern.
As long as you make sure that the appropriate names are defined, it is usually most efficient to put /; conditions on the smallest possible parts of patterns. The reason for this is that the Wolfram Language matches pieces of patterns sequentially, and the sooner it finds a /; condition which fails, the sooner it can reject a match.
Putting the /; condition around the x_ is slightly more efficient than putting it around the whole pattern:
It is common to use /; to set up patterns and transformation rules that apply only to expressions with certain properties. There is a collection of functions built into the Wolfram Language for testing the properties of expressions. It is a convention that functions of this kind have names that end with the letter Q, indicating that they "ask a question".
| IntegerQ[expr] | integer |
| EvenQ[expr] | even number |
| OddQ[expr] | odd number |
| PrimeQ[expr] | prime number |
| NumberQ[expr] | explicit number of any kind |
| NumericQ[expr] | numeric quantity |
| PolynomialQ[expr,{x1,x2,…}] | polynomial in x1, x2, … |
| VectorQ[expr] | a list representing a vector |
| MatrixQ[expr] | a list of lists representing a matrix |
| VectorQ[expr,NumericQ]
,
MatrixQ[expr,NumericQ] | |
vectors and matrices where all elements are numeric | |
| VectorQ[expr,test]
,
MatrixQ[expr,test] | |
vectors and matrices for which the function test yields True on every element | |
| ArrayQ[expr,d] | full array with depth matching d |
An important feature of all the Wolfram Language property‐testing functions whose names end in Q is that they always return False if they cannot determine whether the expression you give has a particular property.
Functions like IntegerQ[x] test whether x is explicitly an integer. With assertions like x∈Integers you can use Refine, Simplify, and related functions to make inferences about symbolic variables x.
| SameQ[x,y] or x===y | x and y are identical |
| UnsameQ[x,y] or x=!=y | x and y are not identical |
| OrderedQ[{a,b,…}] | a, b, … are in standard order |
| MemberQ[expr,form] | form matches an element of expr |
| FreeQ[expr,form] | form matches nothing in expr |
| MatchQ[expr,form] | expr matches the pattern form |
| ValueQ[expr] | a value has been defined for expr |
| AtomQ[expr] | expr has no subexpressions |
With ==, the equation remains in symbolic form; === yields False unless the expressions are manifestly equal:
| pattern?test | a pattern that matches an expression only if test yields True when applied to the expression |
The construction pattern/;condition allows you to evaluate a condition involving pattern names to determine whether there is a match. The construction pattern?test instead applies a function test to the whole expression matched by pattern to determine whether there is a match. Using ? instead of /; sometimes leads to more succinct definitions.
| Except[c] | a pattern that matches any expression except c |
| Except[c,patt] | a pattern that matches patt but not c |
Except can take a pattern as an argument:
Except[c] is in a sense a very general pattern: it matches anything except c. In many situations you instead need to use Except[c,patt], which restricts to expressions matching patt that do not match c.
When you use alternatives in patterns, you should make sure that the same set of names appear in each alternative. When a pattern like (a[x_]|b[x_]) matches an expression, there will always be a definite expression that corresponds to the object x. If you try to match a pattern like (a[x_]|b[y_]), then there still will be definite expressions corresponding to x and y, but the unmatched one will be Sequence[ ].
In some cases you may need to specify pattern sequences that are more intricate than things like x__ or x..; for such situations you can use PatternSequence[p1,p2,…].
| PatternSequence[p1,p2,…] | a sequence of arguments matching p1,p2,… |
The empty sequence, PatternSequence[], is sometimes useful to specify an optional argument.
Although the Wolfram Language matches patterns in a purely structural fashion, its notion of structural equivalence is quite sophisticated. In particular, it takes account of properties such as commutativity and associativity in functions like Plus and Times.
This means, for example, that the Wolfram Language considers the expressions x+y and y+x equivalent for the purposes of pattern matching. As a result, a pattern like g[x_+y_,x_] can match not only g[a+b,a], but also g[a+b,b].
In this case, the expression has to be put in the form g[b+a,b] in order to have the same structure as the pattern:
Whenever the Wolfram Language encounters an orderless or commutative function such as Plus or Times in a pattern, it effectively tests all the possible orders of arguments to try and find a match. Sometimes, there may be several orderings that lead to matches. In such cases, the Wolfram Language just uses the first ordering it finds. For example, h[x_+y_,x_+z_] could match h[a+b,a+b] with x→a, y→b, z→b or with x→b, y→a, z→a. The Wolfram Language tries the case x→a, y→b, z→b first, and so uses this match.
This can match either with x→a or with x→b. The Wolfram Language tries x→a first, and so uses this match:
ReplaceList shows both possible matches:
As discussed in "Attributes", the Wolfram Language allows you to assign certain attributes to functions, which specify how those functions should be treated in evaluation and pattern matching. Functions can for example be assigned the attribute Orderless, which specifies that they should be treated as commutative or symmetric, and allows their arguments to be rearranged in trying to match patterns.
| Orderless | commutative function: f[b,c,a], etc., are equivalent to f[a,b,c] |
| Flat | associative function: f[f[a],b], etc., are equivalent to f[a,b] |
| OneIdentity |
f[f[a]]
, etc., are equivalent to
a
|
| Attributes[f] | give the attributes assigned to f |
| SetAttributes[f,attr] | add attr to the attributes of f |
| ClearAttributes[f,attr] | remove attr from the attributes of f |
In addition to being orderless, functions like Plus and Times also have the property of being flat or associative. This means that you can effectively "parenthesize" their arguments in any way, so that, for example, x+(y+z) is equivalent to x+y+z, and so on.
The Wolfram Language takes account of flatness in matching patterns. As a result, a pattern like g[x_+y_] can match g[a+b+c], with x→a and y→(b+c).
If there are no other constraints, the Wolfram Language will match x_ to the first element of the sum:
The Wolfram Language can usually apply a transformation rule to a function only if the pattern in the rule covers all the arguments in the function. However, if you have a flat function, it is sometimes possible to apply transformation rules even though not all the arguments are covered.
Functions like Plus and Times are both flat and orderless. There are, however, some functions, such as Dot, which are flat, but not orderless.
In an ordinary function that is not flat, a pattern such as x_ matches an individual argument of the function. But in a function f[a,b,c,…] that is flat, x_ can match objects such as f[b,c] which effectively correspond to a sequence of arguments. However, in the case where x_ matches a single argument in a flat function, the question comes up as to whether the object it matches is really just the argument a itself, or f[a]. The Wolfram Language chooses the former possibility if the function carries the attribute OneIdentity, otherwise it will first attempt to use the latter but fall back on the former.
The functions Plus, Times, and Dot all have the attribute OneIdentity, reflecting the fact that Plus[x] is equivalent to x, and so on. However, in representing mathematical objects, it is often convenient to deal with flat functions that do not have the attribute OneIdentity.
Unless f is a flat function, a pattern like f[x_,y_] stands only for instances of the function with exactly two arguments. Sometimes you need to set up patterns that can allow any number of arguments.
You can do this using multiple blanks. While a single blank such as x_ stands for a single Wolfram Language expression, a double blank such as x__ stands for a sequence of one or more expressions.
"Double blanks" __ stand for sequences of one or more expressions. "Triple blanks" ___ stand for sequences of zero or more expressions. You should be very careful whenever you use triple blank patterns. It is easy to make a mistake that can lead to an infinite loop. For example, if you define p[x_,y___]:=p[x] q[y], then typing in p[a] will lead to an infinite loop, with y repeatedly matching a sequence with zero elements. Unless you are sure you want to include the case of zero elements, you should always use double blanks rather than triple blanks.
| _ | any single expression |
| x_ |
any single expression, to be named
x
|
| __ | any sequence of one or more expressions |
| x__ | sequence named x |
| x__h |
sequence of expressions, all of whose heads are
h
|
| ___ | any sequence of zero or more expressions |
| x___ | sequence of zero or more expressions named x |
| x___h |
sequence of zero or more expressions, all of whose heads are
h
|
Notice that with flat functions such as Plus and Times, the Wolfram Language automatically handles variable numbers of arguments, so you do not explicitly need to use double or triple blanks, as discussed in "Flat and Orderless Functions".
When you use multiple blanks, there are often several matches that are possible for a particular expression. By default, the Wolfram Language tries first those matches that assign the shortest sequences of arguments to the first multiple blanks that appear in the pattern. You can change this order by wrapping Longest or Shortest around parts of the pattern.
| Longest[p] | match the longest sequence consistent with the pattern p |
| Shortest[p] | match the shortest sequence consistent with the pattern p |
Many kinds of enumeration can be done by using ReplaceList with various kinds of patterns:
Sometimes you may want to set up functions where certain arguments, if omitted, are given "default values". The pattern x_:v stands for an object that can be omitted, and if so, will be replaced by the default value v.
This defines a function j with a required argument x, and optional arguments y and z, with default values 1 and 2, respectively:
| x_:v |
an expression which, if omitted, is taken to have default value
v
|
| x_h:v | an expression with head h and default value v |
| x_. | an expression with a built‐in default value |
Some common Wolfram Language functions have built‐in default values for their arguments. In such cases, you need not explicitly give the default value in x_:v, but instead you can use the more convenient notation x_. in which a built‐in default value is assumed.
Because Plus is a flat function, a pattern such as x_+y_ can match a sum with any number of terms. This pattern cannot, however, match a single term such as a. However, the pattern x_+y_. contains an optional piece, and can match either an explicit sum of terms in which both x_ and y_ appear, or a single term x_, with y taken to be 0.
Using constructs such as x_., you can easily construct single patterns that match expressions with several different structures. This is particularly useful when you want to match several mathematically equal forms that do not have the same structure.
Standard Wolfram Language functions such as Plus and Times have built‐in default values for their arguments. You can also set up defaults for your own functions, as described in "Patterns".
Sometimes it is convenient not to assign a default value to an optional argument; such arguments can be specified with the help of PatternSequence[].
| p|PatternSequence[] | optional pattern p with no default value |
When you define a complicated function, you will often want to let some of the arguments of the function be "optional". If you do not give those arguments explicitly, you want them to take on certain "default" values.
Built‐in Wolfram Language functions use two basic methods for dealing with optional arguments. You can choose between the same two methods when you define your own functions in the Wolfram Language.
The first method is to have the meaning of each argument determined by its position, and then to allow one to drop arguments, replacing them by default values. Almost all built‐in Wolfram Language functions that use this method drop arguments from the end. For example, the built‐in function Flatten[list,n] allows you to drop the second argument, which is taken to have a default value of Infinity.
| f[x_,k_:kdef]:=value |
a typical definition for a function whose second argument is optional, with default value
kdef
|
This defines a function with an optional second argument. When the second argument is omitted, it is taken to have the default value Infinity:
The Wolfram Language assumes that arguments are dropped from the end. As a result m here gives the value of n1, while n2 has its default value of 2:
The second method that built‐in Wolfram Language functions use for dealing with optional arguments is to give explicit names to the optional arguments, and then to allow their values to be given using transformation rules. This method is particularly convenient for functions like Plot which have a very large number of optional parameters, only a few of which usually need to be set in any particular instance.
The typical arrangement is that values for "named" optional arguments can be specified by including the appropriate transformation rules at the end of the arguments to a particular function. Thus, for example, the rule Joined->True, which specifies the setting for the named optional argument Joined, could appear as ListPlot[list,Joined->True].
When you set up named optional arguments for a function f, it is conventional to store the default values of these arguments as a list of transformation rules assigned to Options[f].
| f[x_,OptionsPattern[]]:=value | a typical definition for a function with zero or more named optional arguments |
| OptionValue[name] | the value of a named optional argument in the body of the function |
Here is the definition for a function fn which allows zero or more named optional arguments to be specified:
| FilterRules[opts,Options[name]] | the rules in opts used as options by the function name |
| FilterRules[opts,Except[Options[name]]] | |
the rules in opts not used as options by the function name | |
This changes the method used by NDSolve and the color in the plot:
| expr.. | a pattern or other expression repeated one or more times |
| expr... | a pattern or other expression repeated zero or more times |
Multiple blanks such as x__ allow you to give patterns in which sequences of arbitrary expressions can occur. The Wolfram Language pattern repetition operators .. and ... allow you to construct patterns in which particular forms can be repeated any number of times. Thus, for example, f[a..] represents any expression of the form f[a], f[a,a], f[a,a,a], and so on.
You can use .. and ... to represent repetitions of any pattern. If the pattern contains named parts, then each instance of these parts must be identical.
The pattern x.. can be extended to two arguments to control the number of repetitions more precisely.
| p.. or Repeated[p] | a pattern or other expression repeated one or more times |
| Repeated[p,max] | a pattern repeated up to max times |
| Repeated[p,{min,max}] | a pattern repeated between min and max times |
| Repeated[p,{n}] | a pattern repeated exactly n times |
| Verbatim[expr] | an expression that must be matched verbatim |
Using the objects described in "Introduction to Patterns", you can set up patterns for many kinds of expressions. In all cases, you must remember that the patterns must represent the structure of the expressions in the Wolfram Language internal form, as shown by FullForm.
Especially for some common kinds of expressions, the standard output format used by the Wolfram Language is not particularly close to the full internal form. But it is the internal form that you must use in setting up patterns.
| n_Integer | an integer n |
| x_Real | an approximate real number x |
| z_Complex | a complex number z |
| Complex[x_,y_] | a complex number x+iy |
| Complex[x_Integer,y_Integer] | a complex number where both real and imaginary parts are integers |
| (r_Rational|r_Integer) | rational number or integer r |
| Rational[n_,d_] | a rational number |
| (x_/;NumberQ[x]&&Im[x]==0) | a real number of any kind |
| (x_/;NumberQ[x]) | a number of any kind |
The fact that these expressions have different full forms means that you cannot use x_+Iy_ to match a complex number:
The pattern here matches both ordinary integers, and complex numbers where both the real and imaginary parts are integers:
As discussed in "Symbolic Computation", the Wolfram Language puts all algebraic expressions into a standard form, in which they are written essentially as a sum of products of powers. In addition, ratios are converted into products of powers, with denominator terms having negative exponents, and differences are converted into sums with negated terms. To construct patterns for algebraic expressions, you must use this standard form. This form often differs from the way the Wolfram Language prints out the algebraic expressions. But in all cases, you can find the full internal form using FullForm[expr].
| x_+y_ | a sum of two or more terms |
| x_+y_. | a single term or a sum of terms |
| n_Integer x_ | an expression with an explicit integer multiplier |
| a_.+b_.x_ | a linear expression a+bx |
| x_^n_ | xn with n≠0,1 |
| x_^n_. | xn with n≠0 |
| a_.+b_.x_+c_.x_^2 | a quadratic expression with nonzero linear term |
| x_List or x:{___} | a list |
| x_List/;VectorQ[x] | a vector containing no sublists |
| x_List/;VectorQ[x,NumberQ] | a vector of numbers |
| x:{___List} or x:{{___}...} | a list of lists |
| x_List/;MatrixQ[x] | a matrix containing no sublists |
| x_List/;MatrixQ[x,NumberQ] | a matrix of numbers |
| x:{{_,_}...} | a list of pairs |
This defines a function whose argument must be a list containing lists with either one or two elements:
Now that we have introduced the basic features of patterns in the Wolfram Language, we can use them to give a more or less complete example. We will show how you could define your own simple integration function in the Wolfram Language.
From a mathematical point of view, the integration function is defined by a sequence of mathematical relations. By setting up transformation rules for patterns, you can implement these mathematical relations quite directly in the Wolfram Language.
mathematical form
| Wolfram Language definition |
| integrate[y_+z_,x_]:=integrate[y,x]+integrate[z,x] | |
| integrate[c_y_,x_]:=c integrate[y,x]/;FreeQ[c,x] | |
| integrate[c_,x_]:=cx/;FreeQ[c,x] | |
| integrate[x_^n_.,x_]:=x^(n+1)/(n+1)/;FreeQ[n,x]&&n!=-1 | |
| integrate[1/(a_.x_+b_.),x_]:=Log[ax+b]/a/;FreeQ[{a,b},x] | |
| integrate[Exp[a_.x_+b_.],x_]:=Exp[ax+b]/a/;FreeQ[{a,b},x] |
The associativity of Plus makes the linearity relation work with any number of terms in the sum:
The Wolfram Language tests each term in each product to see whether it satisfies the FreeQ condition, and so can be pulled out:
This gives the standard formula for the integral of 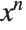 . By using the pattern x_^n_., rather than x_^n_, we include the case of
. By using the pattern x_^n_., rather than x_^n_, we include the case of  :
:
Of course, the built‐in integration function Integrate (with a capital I) could have done the integral anyway: