PairedZTest

PairedZTest[data]

data の平均がゼロであるかどうかを検定する．

PairedZTest[{data1,data2}]

data1および data2の平均が等しいかどうかを検定する．

PairedZTest[dspec,σ]

母分散 σ を想定して，ゼロあるいは等平均であるかを検定する．

PairedZTest[dspec,σ,μ0]

μ0に対して平均を検定する．

PairedZTest[dspec,σ,μ0,"property"]

"property"の値を返す．

詳細とオプション

  • data1と data2について，PairedZTestは2つのデータ集合のペアの差分の検定を行う．
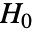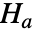  • PairedZTestは，帰無仮説 と対立仮説 で検定を行う．
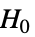
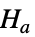
  • data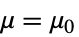
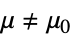
    {data1,data2}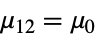
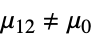
  • ただし，μ は data の母平均であり，μ12は2つのデータ集合のペアになった差分 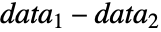の平均である．
  • デフォルトで確率値あるいは 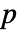値が返される．
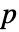  • 値が小さいということは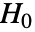，が真である可能性は少ないということである．
  • dspec のデータは，一変量{x1,x2,…}あるいは多変量{{x1,y1,…},{x2,y2,…},…}になりうる．
  • 引数 σ は，任意の正の実数，あるいは data の次元に等しい次元を持つ正定値行列でよい．
  • 引数 μ0は，実数，あるいはデータの次元に等しい長さを持つ実ベクトルでよい．
  • PairedZTestは，data が正規分布に従い，分散が既知でデータから推定されないと仮定する．
  • 分散あるいは共分散の行列が与えられない場合には，PairedZTestはサンプル推定値を既知の分散あるいは共分散として扱う．
  • PairedZTest[dspec,σ,μ0,"HypothesisTestData"]は，形式 htd["property"]を使って追加の検定結果と特性を抽出するのに使えるHypothesisTestDataオブジェクト htd を返す．
  • PairedZTest[dspec,σ,μ0,"property"]を使って"property"の値を直接与えることができる．
  • 検定結果のレポートに関連する特性
  • "DegreesOfFreedom"検定の自由度
    "PValue" 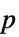値のリスト
    "PValueTable" 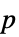値のフォーマットされた表
    "TestData"検定統計と 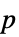値のペアのリスト
    "TestDataTable" 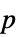値と検定統計のフォーマット化された表
    "TestStatistic"検定統計のリスト
    "TestStatisticTable"検定統計のフォーマット化された表
  • 既知の分散 σ が与えられていない場合には，PairedZTestは，サンプル分散が一変量データの既知の分散であると仮定して 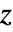検定を行い，サンプル共分散が多変量データの既知の共分散であると仮定してHotellingの 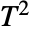検定を行う．
  • オプション
  • AlternativeHypothesis "Unequal"対立仮説のための不等式
    SignificanceLevel 0.05診断とレポートの切捨て
    VerifyTestAssumptions Automaticどの仮定を確かめるのか
  • 位置の検定については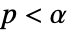， のときに限り 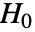が拒絶されるように切捨て 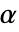が選ばれる．"TestConclusion"および"ShortTestConclusion"の特性に使われる 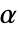の値は，SignificanceLevelオプションで制御される．この値 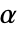は，正規性，等分散，対称性の検定を含む仮定の診断検定にも使われる．デフォルトで 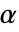は0.05に設定される．
  • PairedZTestにおけるVerifyTestAssumptionsの名前付き設定
  • "Normality"すべてのデータが正規分布に従うことを確かめる

例題

すべて開くすべて閉じる

例  (3)

母集団の平均がゼロであるかどうかを検定する：

完全な検定表：

2つの従属母集団の平均が異なるかどうかを検定する：

差分の平均：

0.05レベルでは，差分データの平均は0とあまり違わない：

従属多変量母集団の位置を比べる：

差分の平均：

0.05レベルでは，差分データの平均は0とあまり変わらない：

スコープ  (13)

検定  (10)

対 を検定する：

平均が μ0に近い場合， 値は通常大きい：

位置が μ0から離れている場合， 値は通常小さい：

Automaticを使うことは，ゼロの平均について検定することと同じである：

対 を検定する：

平均が μ0に近い場合， 値は通常大きい：

位置が μ0から離れている場合， 値は通常小さい：

多変量母集団の平均ベクトルがゼロベクトルであるかどうかを検定する：

{0.1,0,-0.05,0}についても検定する：

差分データ集合の平均がゼロであるかどうかを検定する：

平均がゼロではない場合， 値は一般に小さい：

平均がゼロである場合， 値は一般に大きい：

差分データの平均が3であるかどうかを検定する：

データ集合の順序は検定結果に影響する：

差分多変量データ集合の平均ベクトルがゼロベクトルであるかどうかを検定する：

{1,0,-1,0}についても検定する：

繰り返し特性を抽出するためにHypothesisTestDataオブジェクトを作成する：

抽出に使用できる特性：

HypothesisTestDataオブジェクトから特性を抽出する：

値と検定統計：

任意数の特性を同時に抽出する：

値と検定統計：

レポート  (3)

検定結果を表にする：

カスタマイズしたレポート用に検定表から項目を取り出す：

値か検定統計を表にする：

表の 値：

表の検定統計：

オプション  (8)

AlternativeHypothesis  (3)

デフォルトで両側検定が行われる：

対 を検定する：

両側検定を行う．あるいは片側検定を代りに行う：

対 を検定する：

対 を検定する：

対 を検定する：

μ0が与えられている場合に，片側検定を代りに行う：

対 を検定する：

対 を検定する：

SignificanceLevel  (2)

診断検定の有意水準を設定する：

デフォルトで0.05が使われる：

有意水準は"TestConclusion"と"ShortTestConclusion"にも使われる：

VerifyTestAssumptions  (3)

デフォルトで正規性が検定される：

ここでは正規性が仮定されている：

結果は同じであるが，警告メッセージが出される：

代りにAllを使う：

正規性の仮説をTrueに設定する：

診断検定を使わないと，計算時間が短縮できる：

シミュレーションを行う場合は，診断検定を行わないようにすると有益であることが多い：

検定の仮定は意図的に有効になっているので，時間が大幅に短縮できる：

結果は全く同じである：

アプリケーション  (1)

平均して，人が両手を横に広げたときの幅は，その人の身長に等しい．大学の漕艇チームについて，メンバーが両手を横に広げたときの幅は，彼らの身長よりもかなり大きくなると予想して測定を行った．大人の母集団において身長と両手を横に広げたときの幅の標準偏差は，0.4フィートであると仮定する：

両手を横に広げたときの幅と身長の差の分布の推定：

漕艇チームのメンバーが両手を横に広げたときの幅は，身長よりもずっと大きい：

両手を横に広げたときの幅と身長の比率：

2つの正規確率変数の比率が正規ではないので，この検定にはPairedZTestを使うべきではない：

特性と関係  (6)

1つのデータ集合についてPairedZTestはZTestに等しい：

2つのデータ集合についてPairedZTestはペアの差分のZTestに等しい：

既知の分散：

母分散が既知ではない場合には，あまり強力ではないPairedTTestを使うべきである：

PairedZTestがPairedTTestよりも小さい 値を返す確率：

データを対にすることができる場合には，PairedZTestの方がZTestよりも強力である：

ペアの検定は，ペアではない検定が検出しない部分で有意な差分を検出する：

PairedZTestは，入力がTimeSeriesのときにのみ，値に対して使うことができる：

PairedZTestは，入力がTemporalDataのときはすべての値に使うことができる：

すべての値のみに対して検定を行う：

2つの経路の平均が等しいかどうかの検定を行う：

考えられる問題  (1)

PairedZTestでは，データは正規分布に従わなければならない：

中央値に基づいた検定を使う：

おもしろい例題  (1)

帰無仮説 が真であるときの統計量を計算する：

特定の対立仮説による検定統計：

検定統計の分布を比較する：

Wolfram Research (2010), PairedZTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/PairedZTest.html.

テキスト

Wolfram Research (2010), PairedZTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/PairedZTest.html.

CMS

Wolfram Language. 2010. "PairedZTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PairedZTest.html.

APA

Wolfram Language. (2010). PairedZTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PairedZTest.html

BibTeX

@misc{reference.wolfram_2024_pairedztest, author="Wolfram Research", title="{PairedZTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/PairedZTest.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_pairedztest, organization={Wolfram Research}, title={PairedZTest}, year={2010}, url={https://reference.wolfram.com/language/ref/PairedZTest.html}, note=[Accessed: 18-November-2024 ]}