MannWhitneyTest

MannWhitneyTest[{data1,data2}]

tests whether the medians of data1 and data2 are equal.

MannWhitneyTest[dspec,μ0]

tests the median difference against μ0.

MannWhitneyTest[dspec,μ0,"property"]

returns the value of "property".

Details and Options

  • MannWhitneyTest performs a hypothesis test on data1 and data2 with null hypothesis 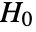that the true median difference 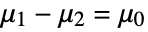agains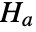t that .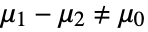
  • By default, a probability value or 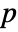-value is returned.
  • A small 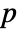-value suggests that it is unlikely that 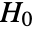is true.
  • The data in dspec can be univariate {x1,x2,…} or multivariate {{x1,y1,…},{x2,y2,…},…}.
  • The argument μ0 can be a real number or a real vector with length equal to the dimension of the data.
  • MannWhitneyTest assumes that the data is elliptically symmetric about a common spatial median in the multivariate case.
  • MannWhitneyTest[dspec,μ0,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
  • MannWhitneyTest[dspec,μ0,"property"] can be used to directly give the value of "property".
  • Properties related to the reporting of test results include:
  • "DegreesOfFreedom"the degrees of freedom used in a test
    "PValue"list of 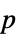-values
    "PValueTable"formatted table of 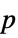-values
    "ShortTestConclusion"a short description of the conclusion of a test
    "TestConclusion"a description of the conclusion of a test
    "TestData"list of pairs of test statistics and 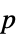-values
    "TestDataTable"formatted table of 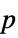-values and test statistics
    "TestStatistic"list of test statistics
    "TestStatisticTable"formatted table of test statistics
  • The following options can be used:
  • AlternativeHypothesis "Unequal"the inequality for the alternative hypothesis
    MaxIterations Automaticmax iterations for multivariate median tests
    Method Automaticthe method to use for computing 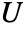-values
    SignificanceLevel 0.05cutoff for diagnostics and reporting
  • For univariate samples, MannWhitneyTest performs the Mann–Whitney 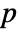-test for median differences of independent samples. The following methods are available:
  • Automaticchooses depending on the size of the sample
    "Asymptotic"large sample statistic is asymptotically normally distributed
    "Exact"small sample 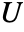values can be computed exactly
    "Permutation"simulation based
  • For the "Asymptotic" and "Permutation" methods, a correction for ties is applied; the test statistic is corrected for continuity, and it is assumed to follow a NormalDistribution.
  • For multivariate samples, MannWhitneyTest performs an extension of the Mann–Whitney 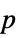-test using spatial ranks. The test statistic is assumed to asymptotically follow a ChiSquareDistribution[dim] where dim is the dimension of dspec.
  • For the MannWhitneyTest, a cutoff 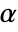is chosen such that 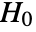is rejected only if 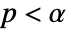. The value of 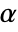used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. By default, 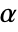is set to 0.05.

Examples

open allclose all

Basic Examples  (2)

Test whether the medians of two independent populations differ:

The median difference :

At the 0.05 level, the medians are significantly different:

Compare the locations of multivariate populations:

The median difference vector :

At the 0.05 level, is not significantly different from {1,2}:

Scope  (9)

Testing  (6)

Test versus :

The -values are generally small when the locations are not equal:

The -values are generally large when the locations are equal:

Test versus :

The order of the datasets affects the test results:

Test whether the median difference vector of two multivariate populations is the zero vector:

Alternatively, test against {1,0,-1,0}:

Create a HypothesisTestData object for repeated property extraction:

The properties available for extraction:

Extract some properties from a HypothesisTestData object:

The -value and test statistic:

Extract any number of properties simultaneously:

The -value and test statistic from a Mann–Whitney test:

Reporting  (3)

Tabulate the test results:

Retrieve the entries from a test table for customized reporting:

Tabulate -values or test statistics:

The -value from the table:

The test statistic from the table:

Generalizations & Extensions  (2)

The Mann–Whitney test ignores the time stamps when the input is a TimeSeries:

The Mann–Whitney test recognizes the path structure of a TemporalData with exactly two paths:

Use the values directly:

Options  (12)

AlternativeHypothesis  (4)

A two-sided test is performed by default:

Test versus :

Perform a two-sided test or a one-sided alternative:

Test versus :

Test versus :

Test versus :

Perform tests with one-sided alternatives when μ0 is given:

Test versus :

Test versus :

The two-sided test is symmetric under the exchange of the datasets:

The one-sided tests are not symmetric under the exchange of the datasets:

However, for the permutation method even the (default) two-sided test is not symmetric:

MaxIterations  (2)

Set the maximum number of iterations to use for multivariate tests:

By default, 250 iterations are allowed:

Setting the maximum number of iterations may result in lack of convergence:

The -values are not equivalent:

Method  (5)

For small samples, -values are computed using an exact formula by default:

For large samples, -values are computed using asymptotic test statistic distributions by default:

Permutation methods can be used:

Set the number of permutations to use:

By default, random permutations are used:

Set the seed used for generating random permutations:

SignificanceLevel  (1)

The significance level is used for "TestConclusion" and "ShortTestConclusion":

Applications  (3)

Test whether the medians of some populations are equal:

The medians of the first two populations are similar:

The median of the third population is different from the first:

It has been observed that the duration of Old Faithful geyser eruptions is proportional to the time elapsed since the previous eruption:

Assuming one hour is a long wait for an eruption, test the statement that long waits lead to long eruption durations:

Two hundred Australian crabs were collected, and five morphological measures were taken for each crab. The data is organized by type and gender:

Determine if there is a difference in the first four morphological measures for the two varieties:

Compare the morphological measures across the genders:

Properties & Relations  (4)

For univariate data, the test statistic follows a NormalDistribution[0,1] under :

A large sample approximation to the NormalDistribution:

For multivariate data, the test statistic follows a ChiSquareDistribution[dim] under :

The test statistic is computed by pooling and ranking the data:

In the absence of ties, Ordering can compute the ranks:

The exact -value matches the frequencies of the test statistic when considering every possible permutation for a given size of the datasets:

Show few permutations:

Compute the statistics and -values for all the permutation pairs:

Show few results:

Compute frequencies by normalizing the counts of the statistic:

The statistic is an integer between and the product of the lengths of the data inputs—here :

Since the -value is the cumulative mass function (CDF) of the test distribution, it needs to be compared to the cumulative frequencies:

By convention, the -values start at :

The exact -value is computed using the following recursion relation:

Possible Issues  (1)

For the permutation method, the two-sided test is not symmetric under the exchange of the datasets:

Neat Examples  (1)

Compute the statistic when the null hypothesis is true:

The test statistic given a particular alternative:

Compare the distributions of the test statistics:

Wolfram Research (2010), MannWhitneyTest, Wolfram Language function, https://reference.wolfram.com/language/ref/MannWhitneyTest.html.

Text

Wolfram Research (2010), MannWhitneyTest, Wolfram Language function, https://reference.wolfram.com/language/ref/MannWhitneyTest.html.

CMS

Wolfram Language. 2010. "MannWhitneyTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MannWhitneyTest.html.

APA

Wolfram Language. (2010). MannWhitneyTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MannWhitneyTest.html

BibTeX

@misc{reference.wolfram_2025_mannwhitneytest, author="Wolfram Research", title="{MannWhitneyTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/MannWhitneyTest.html}", note=[Accessed: 18-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_mannwhitneytest, organization={Wolfram Research}, title={MannWhitneyTest}, year={2010}, url={https://reference.wolfram.com/language/ref/MannWhitneyTest.html}, note=[Accessed: 18-March-2025 ]}