PermutationProduct[a,b,c]
gives the product of permutations a, b, c.


PermutationProduct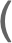

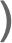
PermutationProduct[a,b,c]
gives the product of permutations a, b, c.
Details
- The product of permutations a, b, c is understood to be the permutation resulting from applying a, then b, then c.
- PermutationProduct[g1,g2,…,gn] gives the left-to-right product of n permutations.
- The product of permutations is non-commutative.
- PermutationProduct[g] gives g.
- PermutationProduct[] returns the identity permutation Cycles[{}].
- PermutationProduct[a,b] can be input as ab. The character is entered as
 p*
p* or \[PermutationProduct].
or \[PermutationProduct].
Examples
open all close allScope (4)
PermutationProduct works with any number of permutations, of any degree:
Product of a single permutation:
Generalizations & Extensions (3)
PermutationProduct performs some simplifications with symbolic arguments:
Perform intermediate products:
From the product and inversion in a group, it is possible to define commutation and conjugation as follows. Use this abbreviation:
Two permutations commute if and only if their commutator is the identity:
Commutation can be recursively generalized to more arguments:
Properties & Relations (5)
Multiplication with the inverse permutation returns the identity:
Any cycle of length ![]() is equivalent to a product of
is equivalent to a product of ![]() transpositions (cycles of length 2) all having the same first point:
transpositions (cycles of length 2) all having the same first point:
Multiplication of permutation lists is equivalent to Part but reversing the order:
Repeated multiplication of a single permutation can be computed with PermutationPower:
The product of all elements of a group depends on the order in which the product is computed:
For an Abelian group, the result is unique. In particular, for a cyclic group the result is very simple:
The result is simply this power of the generator of the cyclic group:
Possible Issues (1)
PermutationProduct[x] returns x, irrespectively of what x is:
See Also
Cycles PermutationPower PermutationReplace Permute GroupMultiplicationTable
Characters: \[PermutationProduct]
Tech Notes
Related Guides
History
Text
Wolfram Research (2010), PermutationProduct, Wolfram Language function, https://reference.wolfram.com/language/ref/PermutationProduct.html.
CMS
Wolfram Language. 2010. "PermutationProduct." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PermutationProduct.html.
APA
Wolfram Language. (2010). PermutationProduct. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PermutationProduct.html
BibTeX
@misc{reference.wolfram_2025_permutationproduct, author="Wolfram Research", title="{PermutationProduct}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/PermutationProduct.html}", note=[Accessed: 09-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_permutationproduct, organization={Wolfram Research}, title={PermutationProduct}, year={2010}, url={https://reference.wolfram.com/language/ref/PermutationProduct.html}, note=[Accessed: 09-January-2026]}