Permutations
Permutations
| Representation of a Permutation | Product of Permutations |
| Permutation Action and Support | Equality and Sorting of Permutations |
| Permute Parts of an Expression | Special Types of Permutations |
Permutations are basic elements in algebra. They have a natural non-commutative product (as matrices do as well), and hence can encode highly nontrivial structures in a compact way. Permutations provide a way of representing any finite group, which makes them key tools in many applications in mathematics, science, engineering, or even art. In particular, permutations play a central role in the description of discrete symmetries.
Permutations are, roughly speaking, reorderings of a set of elements, or more precisely, bijections from the set onto itself. Only sets with a finite number of elements will be considered. The number of possible permutations of a set of 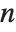 elements is
elements is 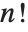 , and therefore for a moderate number
, and therefore for a moderate number 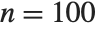 there are already
there are already 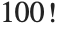 permutations, which is almost
permutations, which is almost 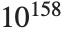 .
.
This tutorial discusses how to manipulate permutations in cyclic notation in the Wolfram Language, and "Permutation Lists" describes the relation to permutation list notation. Other tutorials, "Permutation Groups" and "Named Groups", describe how to work with groups of permutations, and "Group Theory Algorithms" shows how to extract information from them without listing all elements of the group.
| Cycles | head denoting a permutation in disjoint cyclic form |
| PermutationCyclesQ | validate a permutation |
The disjoint cyclic representation of a permutation has the form Cycles[{cyc1,cyc2,…}] in the Wolfram Language, where the cycles cyci are disjoint lists of positive integers. Integers are mapped under the permutation to their right neighbors, and the last integer of a cycle is mapped to the first member of that cycle. Integers not present in the cycles are mapped onto themselves, though they could also appear in cycles of length 1, which are called singletons or fixed points. The ordering of cycles is immaterial, and individual cycles can be rotated without changing the permutation. Permutations are automatically canonicalized so that the smallest integer of each cycle comes first, and then cycles are sorted by their first integer.
With permutations containing explicit lists of numbers, there is automatic syntax checking. In other cases, you can use the function PermutationCyclesQ to check the syntax.
If a permutation perm maps the integer 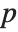 to the integer
to the integer 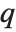 , then
, then 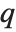 is called the image of
is called the image of 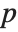 under the permutation perm. Images are computed with the function PermutationReplace.
under the permutation perm. Images are computed with the function PermutationReplace.
| PermutationReplace | image of an integer under a permutation |
The standard action of permutations can be extended to other objects, like other permutations or arrays of integers or permutations.
Permutations are not assumed to belong to any particular finite group, not even a particular symmetric group of some degree. However, there is the concept of support, defined as the set of integers moved by the permutation, which better describes where a permutation acts naturally.
| PermutationSupport | set of integers moved by a permutation |
| PermutationLength | number of integers moved by a permutation |
| PermutationMax | largest integer moved by a permutation |
| PermutationMin | smallest integer moved by a permutation |
| RandomPermutation | generate pseudorandom permutations |
Permutations can be used to permute the parts of other expressions with the function Permute. Integer 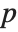 being mapped to integer
being mapped to integer 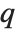 is interpreted as part
is interpreted as part 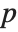 being moved to part
being moved to part 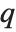 . Permute never changes the number of elements of an expression, it simply reorders them.
. Permute never changes the number of elements of an expression, it simply reorders them.
| Permute | permute parts of an expression |
| FindPermutation | return permutation linking two expressions with the same elements |
The same result can be obtained using a permutation list representation and the function Part:
Permutation lists can also be used with the function Permute:
Vice versa, given two expressions with the same elements, a permutation linking them can be computed:
With a single argument, FindPermutation returns the permutation that generates an expression from its canonical order:
| PermutationProduct |
product of permutations (non-commutative)
|
| InversePermutation | inverse of a permutation |
| PermutationPower |
integer power (product with itself or inverse) of a permutation
|
| PermutationOrder | lowest positive power of a permutation yielding the identity |
There are two possible conventions for the product of two permutations perm1 and perm2, depending on whether PermutationProduct[perm1,perm2] means that you first use perm1 and then perm2 (this is called a left-to-right product) or you first use perm2 and then perm1 (right-to-left product). With the convention of writing images as right neighbors in cycles, the Wolfram Language's PermutationProduct effectively is a left-to-right product.
PermutationReplace acts from the right, consistent with the left-to-right character of the product:
Permute also acts from the right:
After the permutation product law has been given, the associated concepts of inversion, power, and order can be immediately defined. For permutations of finite support, the order is always finite.
The order of a permutation is the lowest positive power such that the identity permutation is obtained:
This means that (for permutations of finite support) the inverse is always a positive power of the permutation:
As is standard in the Wolfram Language, there are two types of equality tests: structural equality (SameQ) and mathematical equality (Equal). The former can compare any two expressions, but the latter will only return True or False when comparing mathematical expressions with the same type of value. The same happens when ordering expressions: there is structural (canonical) order, implemented through Order and OrderedQ, and there is mathematical order, given by Less and related functions.
Any two permutations of any degree can always be tested for equality and ordering. This is done by comparing sequentially the images of the integers 1, 2, 3, … . The smaller permutation corresponds to smaller images, such that the identity permutation always comes first. This defines mathematical order. Canonical order follows standard rules, and may differ from mathematical order.
There are special types of permutations. In many cases the cyclic notation allows simple constructions to detect them.
From the cyclic notation of a permutation it is also simple to construct a decomposition into transpositions, that is, permutations with a single cycle of length 2.