PermutationProduct

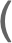
PermutationProduct[a,b,c]

a，b，c の置換の積を与える．

詳細

例題

すべて開くすべて閉じる

例  (1)

2つの置換の積：

置換の乗法は可換ではない：

スコープ  (4)

PermutationProductは任意の次数について任意の数の置換に使うことができる：

1つの置換の積：

恒等置換の乗算：

次は恒等置換を与える：

一般化と拡張  (3)

PermutationProductは記号引数について何らかの簡約を行う：

中間の積を出す：

群内の積と反転から交換子と共役作用素を定義することができる．以下の短縮を使う：

定義する：

交換子が恒等式のときかつそのときに限り2つの置換は可換である：

交換は反復的により多くの引数について一般化される：

よく知られた交換関係を調べる：

特性と関係  (5)

逆置換を含む乗法は恒等式を返す：

長さ の任意の巡回はすべてが同じ初期点を持つ 転置（長さ2の巡回）の積に等しい：

置換リストの乗法はPartに等しいが順序は逆になる：

1つの置換の反復的な乗算はPermutationPowerで計算することができる：

群のすべての元の積は積が計算される順序に依存する：

アーベル群では，結果が一意的である．特に，巡回群では結果が非常に単純である：

結果は単に巡回群の生成元のベキである：

考えられる問題  (1)

PermutationProduct[x]は x が何であるかに関係なく x を返す：

Wolfram Research (2010), PermutationProduct, Wolfram言語関数， https://reference.wolfram.com/language/ref/PermutationProduct.html.

テキスト

Wolfram Research (2010), PermutationProduct, Wolfram言語関数， https://reference.wolfram.com/language/ref/PermutationProduct.html.

CMS

Wolfram Language. 2010. "PermutationProduct." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PermutationProduct.html.

APA

Wolfram Language. (2010). PermutationProduct. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PermutationProduct.html

BibTeX

@misc{reference.wolfram_2024_permutationproduct, author="Wolfram Research", title="{PermutationProduct}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/PermutationProduct.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_permutationproduct, organization={Wolfram Research}, title={PermutationProduct}, year={2010}, url={https://reference.wolfram.com/language/ref/PermutationProduct.html}, note=[Accessed: 22-November-2024 ]}