PlaneCurveData
PlaneCurveData[entity,property]
平面曲線 entity について,指定された property の値を与える.
PlaneCurveData[{entity1,entity2,…},property]
指定された平面曲線実体の特性値のリストを与える.
PlaneCurveData[entity,property,annotation]
指定された property に関連する指定された annotation を与える.
詳細



- PlaneCurveData[]は,すべての平面曲線実体のリストを与える.
- PlaneCurveData["Properties"]は,使用可能な特性のリストを与える.
- PlaneCurveData["SampleEntities"]は,サンプル実体のリストを与える.
- PlaneCurveData中で指定される entity は,Entity,EntityClass,実体の正規名,あるいはそれらのリストでよい.
- property としては,EntityProperty,EntityPropertyClass,実体の正規名,あるいはそれらのリストを指定することができる.
- 特定のケースで適用できない,あるいは未知である実体は,Missing[…]で示される.
- 特性
-
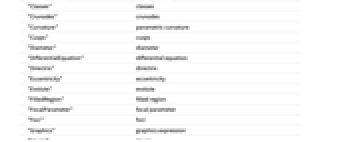
"Acnodes" 孤立点 "AlgebraicDegree" 代数次数 "AlgebraicEquation" 代数式 "AlternateNames" 別名 "ArcLength" 弧長 "ArcLengthFunction" 弧長関数 "Area" 囲み込まれた面積 "AreaImage" 面積を囲み込んだプロット "AreaMomentOfInertiaTensor" 囲い込まれたラミナの慣性テンソルの面積モーメント "AssociatedEntities" 関連する実体 "AssociatedPeople" 関連する人 "Asymptotes" 漸近線 "CartesianEquation" デカルト方程式 "Centroid" 囲い込まれたラミナの重心 "CesaroEquation" Cesàro方程式 "ChordLength" 弦長 "Circumference" 外周 "Classes" クラス "Crunodes" 結節点 "Curvature" パラメトリック曲率 "Cusps" 尖点 "Diameter" 直径 "DifferentialEquation" 微分方程式 "Directrix" 準線 "Eccentricity" 離心率 "Evolute" 縮閉線 "FilledRegion" 充填領域 "FocalParameter" 焦点パラメータ "Foci" 焦点 "Graphics" グラフィックス式 "Image" 画像 "ImplicitCurvature" 陰的曲率 "ImplicitSlope" 陰的勾配 "ImplicitVectorLength" 陰的ベクトル長 "InfinitePoints" 無限点 "InflectionPoints" 変曲点 "Involute" 伸開線 "LatusRectum" 通径 "LineSegmentLengthCDF" 長さの累積分布関数 "LineSegmentLengthMean" 平均線分の長さ "LineSegmentLengthPDF" 長さの確率密度関数 "MajorAxis" 長軸の長さ(外径) "MinorAxis" 短軸の長さ(内径) "Name" 名称 "NaturalParametricEquations" 自然パラメトリック方程式 "NodeCount" ノード数 "NormalVector" 法線ベクトル "NotationTable" 表記法の表 "ParallelCurve" 平行曲線 "Parameters" パラメータ "ParametricEquations" パラメータ方程式 "PedalCurve" 垂足曲線 "Period" 周期 "PolarCurvature" 極曲率 "PolarEquation" 極方程式 "PolarSlope" 極勾配 "QuadruplePoints" 四重点 "Radius" 半径 "RamphoidCusps" Ramphoid尖端 "RelatedWolframLanguageSymbols" Wolfram言語内の関連シンボル "SalientPoints" 凸角点 "SemialgebraicDescription" 半代数的表示 "SemilatusRectum" 半通径 "SemimajorAxis" 長半径 "SemiminorAxis" 短半径 "SignedArea" 囲み込まれた符号付きの面積 "SingularPoints" 特異点 "Slope" パラメトリック勾配 "SpecialAffineCurvature" 特殊なアフィン曲率 "SpecialCases" 特殊例 "Tacnodes" 二重尖点 "TangentialAngle" 正接角 "TangentVector" 接ベクトル "TriplePoints" 三重点 "VariableConstraints" 変数の制約 "VariableDescriptions" 変数の説明 "Variables" 変数 "VectorLength" ベクトル長 "WhewellEquation" Whewell方程式
例題
すべて開くすべて閉じる例 (8)
特性と関係 (2)
PlaneCurveDataを使うことは,対応する実体と特性についてEntityValueを呼ぶことに等しい:
"Classes"引数を付けてPlaneCurveDataを評価する:
上記は実体タイプが"PlaneCurve"のEntityClassListを評価することに等しい:
考えられる問題 (1)
明示的なEntityClassを指定すると思った通りに動作する:
これは,EntityClassについてEntityListを呼ぶことと等価である:
テキスト
Wolfram Research (2014), PlaneCurveData, Wolfram言語関数, https://reference.wolfram.com/language/ref/PlaneCurveData.html (2019年に更新).
CMS
Wolfram Language. 2014. "PlaneCurveData." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/PlaneCurveData.html.
APA
Wolfram Language. (2014). PlaneCurveData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PlaneCurveData.html