PolygonalNumber

PolygonalNumber[n]

gives the n^(th) triangular number .

PolygonalNumber[r,n]

gives the n^(th) r-gonal number .

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • PolygonalNumber[n] is generically defined as TemplateBox[{{n, +, 1}, 2}, Binomial].
  • PolygonalNumber[r,n] is generically defined as .
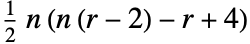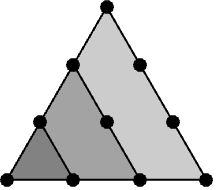
  • PolygonalNumber[r,n] can be interpreted as the number of points arranged in the form of n-1 polygons of r sides. For instance for r=3 and n=4:
  • PolygonalNumber automatically threads over lists.

Examples

open allclose all

Basic Examples  (2)

Return the first 10 triangular numbers:

Return the tenth r-gonal number of several regular polygons:

Scope  (4)

Use PolygonalNumber with integer arguments:

Use RegularPolygon to specify the number of sides of a regular polygon:

PolygonalNumber automatically threads over lists:

Use PolygonalNumber with symbolic input:

Applications  (2)

Generate random octagonal numbers:

Plot the first 50 triangular, square, and pentagonal numbers:

Properties & Relations  (9)

The 0^(th) polygonal number of any regular polygon is zero:

The first polygonal number of any regular polygon is one:

Every other triangular number is a hexagonal number:

The sum of two consecutive triangular numbers is a square number:

Every pentagonal number is one third of a triangular number:

The difference between the n^(th) r-gonal number and the n^(th) (r+1)-gonal number is the (n-1)^(th) triangular number:

Even perfect numbers are triangular numbers related to Mersenne prime exponents:

Even perfect numbers are hexagonal numbers related to Mersenne prime exponents:

All even perfect numbers greater than 6 are of the following form for some value of k:

Neat Examples  (1)

Visualize polygonal numbers:

Wolfram Research (2016), PolygonalNumber, Wolfram Language function, https://reference.wolfram.com/language/ref/PolygonalNumber.html.

Text

Wolfram Research (2016), PolygonalNumber, Wolfram Language function, https://reference.wolfram.com/language/ref/PolygonalNumber.html.

CMS

Wolfram Language. 2016. "PolygonalNumber." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PolygonalNumber.html.

APA

Wolfram Language. (2016). PolygonalNumber. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PolygonalNumber.html

BibTeX

@misc{reference.wolfram_2024_polygonalnumber, author="Wolfram Research", title="{PolygonalNumber}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/PolygonalNumber.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_polygonalnumber, organization={Wolfram Research}, title={PolygonalNumber}, year={2016}, url={https://reference.wolfram.com/language/ref/PolygonalNumber.html}, note=[Accessed: 21-November-2024 ]}