gives the regular polygon with n vertices equally spaced around the unit circle.
RegularPolygon[r,n]
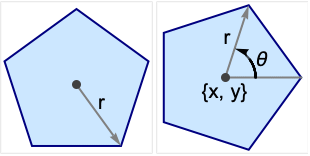
gives the regular polygon of radius r.
RegularPolygon[{r,θ},n]
starts at angle θ with respect to the ![]() axis.
axis.
RegularPolygon[{x,y},rspec,n]
centers the polygon at {x,y}.


RegularPolygon
gives the regular polygon with n vertices equally spaced around the unit circle.
RegularPolygon[r,n]
gives the regular polygon of radius r.
RegularPolygon[{r,θ},n]
starts at angle θ with respect to the ![]() axis.
axis.
RegularPolygon[{x,y},rspec,n]
centers the polygon at {x,y}.
Details and Options

- RegularPolygon can be used as a geometric region and a graphics primitive.
- The angle θ is measured in radians counterclockwise from the positive x direction.
- RegularPolygon for integer n represents a polygon with equal angles between subsequent points.
- CanonicalizePolygon can be used to convert a regular polygon to an explicit Polygon object.
- RegularPolygon can be used in Graphics.
- In graphics, the point {x,y} can be Scaled, Offset, ImageScaled, and Dynamic expressions and the radius r can be Scaled, ImageScaled, and Dynamic.
- Graphics rendering is affected by directives such as FaceForm, EdgeForm, and color.
Examples
open all close allBasic Examples (3)
Scope (17)
Applications (4)
Create a star region by taking the RegionUnion of rotated triangles about a common origin:
Create 3D extrusions with RegionProduct:
Plot a function over a hexagon:
Some lattices will have regular polygons as their cells. Consider the lattice basis:
Properties & Relations (3)
A RegularPolygon is a Polygon whose ![]() vertices are equally spaced around the unit circle:
vertices are equally spaced around the unit circle:
Use CirclePoints to generate points equally spaced around the unit circle:
The area of a regular polygon on the unit circle as ![]() is the area of a unit Disk:
is the area of a unit Disk:
See Also
CirclePoints Polygon Triangle Rectangle
Function Repository: RegularPolygonAngleRadius PolygonFromBase
Related Guides
Text
Wolfram Research (2015), RegularPolygon, Wolfram Language function, https://reference.wolfram.com/language/ref/RegularPolygon.html (updated 2019).
CMS
Wolfram Language. 2015. "RegularPolygon." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/RegularPolygon.html.
APA
Wolfram Language. (2015). RegularPolygon. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RegularPolygon.html
BibTeX
@misc{reference.wolfram_2025_regularpolygon, author="Wolfram Research", title="{RegularPolygon}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/RegularPolygon.html}", note=[Accessed: 09-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_regularpolygon, organization={Wolfram Research}, title={RegularPolygon}, year={2019}, url={https://reference.wolfram.com/language/ref/RegularPolygon.html}, note=[Accessed: 09-January-2026]}