PolygonalNumber

PolygonalNumber[n]

n 番目の三角数 を与える．

PolygonalNumber[r,n]

n 番目の r 角数 を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • PolygonalNumber[n]は，一般に，TemplateBox[{{n, +, 1}, 2}, Binomial]と定義できる．
  • PolygonalNumber[r,n]は，一般に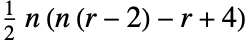，と定義できる．
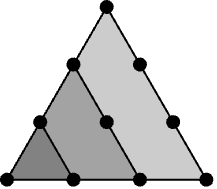
  • PolygonalNumber[r,n]は，r 本の辺を有する n-1多角形の形に並べられた点の数として解釈することができる．例えば r=3で n=4の場合は以下となる．
  • PolygonalNumberは自動的にリストに縫い込まれる．

例題

すべて開くすべて閉じる

例  (2)

最初の10個の三角数を返す：

いくつかの正多角形の10番目の r 角数を返す：

スコープ  (4)

PolygonalNumberを整数の引数とともに使う：

RegularPolygonを使って正多角形の辺の数を指定する：

PolygonalNumberは自動的にリストに縫い込まれる：

PolygonalNumberを記号入力とともに使う：

アプリケーション  (2)

八角数をランダムに生成する：

最初の50個の三角数，四角数，五角数をプロットする：

特性と関係  (9)

任意の多角形の0番目の多角数は0である：

任意の正多角形の最初の多角数は1である：

三角数は1つおきに六角数である：

連続する2つの三角数の和は四角数である：

五角数はすべて三角数の三分の1である：

n 番目の r 角数と n 番目の (r+1)角数の差は(n-1)番目の三角数である：

偶数の完全数はメルセンヌ素数指数に関連している三角数である：

偶数の完全数はメルセンヌ素数指数に関連している六角数である：

6より大きいすべての完全数は，k のある値について次の形式を取る：

おもしろい例題  (1)

多角数を可視化する：

Wolfram Research (2016), PolygonalNumber, Wolfram言語関数， https://reference.wolfram.com/language/ref/PolygonalNumber.html.

テキスト

Wolfram Research (2016), PolygonalNumber, Wolfram言語関数， https://reference.wolfram.com/language/ref/PolygonalNumber.html.

CMS

Wolfram Language. 2016. "PolygonalNumber." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PolygonalNumber.html.

APA

Wolfram Language. (2016). PolygonalNumber. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PolygonalNumber.html

BibTeX

@misc{reference.wolfram_2024_polygonalnumber, author="Wolfram Research", title="{PolygonalNumber}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/PolygonalNumber.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_polygonalnumber, organization={Wolfram Research}, title={PolygonalNumber}, year={2016}, url={https://reference.wolfram.com/language/ref/PolygonalNumber.html}, note=[Accessed: 22-November-2024 ]}